
【题目】如图,在Rt△ABC中,∠C = 90°,点O是斜边AB上一定点,到点O的距离等于OB的所有点组成图形W,图形W与AB,BC分别交于点D,E,连接AE,DE,∠AED=∠B.

(1)判断图形W与AE所在直线的公共点个数,并证明.
(2)若![]() ,
,![]() ,求OB.
,求OB.
【答案】(1)有一个公共点,证明见解析;(2)![]() .
.
【解析】
(1)先根据题意作出图形W,再作辅助线,连接OE,证明AE是圆O的切线即可;
(2)先利用解直角三角形的知识求出CE=1,从而求出BE=3.再由AC∥DE 得出![]() ,把各线段的长代入即可求出OB的值.
,把各线段的长代入即可求出OB的值.
(1)判断有一个公共点
证明:连接OE,如图.
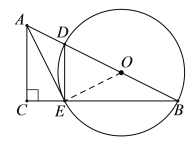
∵ BD是⊙O的直径,
∴ ∠DEB=90°.
∵ OE=OB,
∴ ∠OEB=∠B.
又∵∠AED=∠B,
∴ ∠AED=∠OEB.
∴ ∠AEO =∠AED+∠DEO
=∠OEB +∠DEO
=∠DEB=90°.
∴ AE是⊙O的切线.
∴图形W与AE所在直线有1个公共点.
(2)解:∵ ∠C = 90°,![]() ,
,![]() ,
,
∴ AC=2,![]() .
.
∵ ∠DEB=90°,
∴ AC∥DE.
∴ ![]() ∠CA E=
∠CA E=![]() ∠AED=
∠AED=![]() B
B ![]() .
.
在Rt△ACE中,∠C = 90°,AC=2,
∴ CE=1.
∴ BE=3.
∵AC∥DE
∴![]() .
.
∴![]() ,
,
∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕点A顺时针旋转θ(0°≤θ≤360°),得到矩形AEFG.
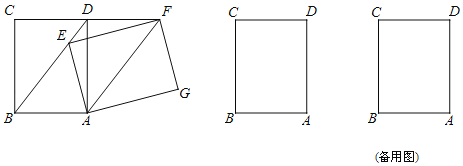
(1)当点E在BD上时,求证:AF∥BD;
(2)当GC=GB时,求θ;
(3)当AB=10,BG=BC=13时,求点G到直线CD的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2-12ax+36a-5的图象在4<x<5这一段位于x轴下方,在8<x<9这一段位于x轴上方,则a的值为___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某班同学随机投掷一枚硬币的试验结果.
抛掷次数 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
“正面向上”次数 | 22 | 52 | 68 | 101 | 116 | 147 | 160 | 187 | 214 | 238 |
“正面向上”频率 | 0.44 | 0.52 | 0.45 | 0.51 | 0.46 | 0.49 | 0.46 | 0.47 | 0.48 | 0.48 |
下面有三个推断:
①表中没有出现“正面向上”的频率是0.5的情况,所以不能估计“正面向上”的概率是0.5;
②这些次试验投掷次数的最大值是500,此时“正面向上”的频率是0.48,所以“正面向上”的概率是0.48;
③投掷硬币“正面向上”的概率应该是确定的,但是大量重复试验反映的规律并非在每一次试验中都发生;
其中合理的是__________(填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
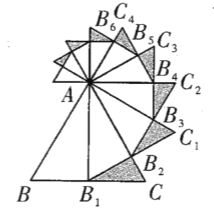
【题目】如图,已知等边![]() 的边长是
的边长是![]() ,以
,以![]() 边上的高
边上的高![]() ,为边作等边三角形,得到第一个等边
,为边作等边三角形,得到第一个等边![]() ;再以等边
;再以等边![]() 的
的![]() 边上的高
边上的高![]() ,为边作等边三角形,得到第二个等边
,为边作等边三角形,得到第二个等边![]() ,再以等边
,再以等边![]() 的
的![]() 边上的高
边上的高![]() 为边作等边三角形,得到第三个等边
为边作等边三角形,得到第三个等边![]() : ....记
: ....记![]() 的面积为
的面积为![]() 的面积为
的面积为![]() 的面积为
的面积为![]() ,如此下去,则
,如此下去,则![]() ___________
___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年湖南省进入高中学习的学生三年后将面对新高考,高考方案与高校招生政策都将有重大变化。某部门为了了解政策的宣传情况,对某初级中学学生进行了随机抽样调查,根据学生对政策的了解程度由高到低分为A,B,C,D四个等级,并对调查结果分析后绘制了如下两幅图不完整的统计图。请你根据图中提供的信息完成下列问题:
(1)求被调查学生的人数,并将条形统计图补充完整;
(2)求扇形统计图中的A等对应的扇形圆心角的度数;
(3)已知该校有1500名学生,估计该校学生对政策内容了解程度达到A等的学生有多少人?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com