
【题目】如图,将矩形ABCD绕点A顺时针旋转θ(0°≤θ≤360°),得到矩形AEFG.
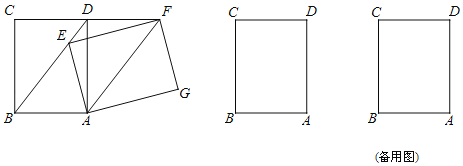
(1)当点E在BD上时,求证:AF∥BD;
(2)当GC=GB时,求θ;
(3)当AB=10,BG=BC=13时,求点G到直线CD的距离.
【答案】(1)见解析;(2)60°或300°;(3)25或1
【解析】
(1)先运用SAS判定△FEA≌△DAB,可得∠AFE=∠ADE=∠DEF,即可得出AF∥BD;
(2)当GB=GC时,点G在BC的垂直平分线上,分两种情况讨论,依据∠DAG=60°,即可得到旋转角θ的度数.
(3)当BG=BC时存在两种情况:画图根据勾股定理计算即可.
(1)由旋转可得,AE=AB,∠AEF=∠DAB=90°,EF=BC=AD,
∴∠AEB=∠ABE,△FEA≌△DAB(SAS),
∴∠AFE=∠ADB,
又∵∠ABE+∠EDA=90°=∠AEB+∠DEF,
∴∠EDA=∠DEF,
∴∠DEF=∠AFE,
∴AF∥BD;
(2)如图1,当GB=GC时,点G在BC的垂直平分线上,分两种情况讨论:
①当点G在AD右侧时,取BC的中点H,连接GH交AD于M,连接DG,
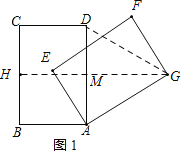
∵GC=GB,
∴GH⊥BC,
∴四边形ABHM是矩形,
∴AM=BH=![]() AD=
AD=![]() AG,
AG,
∴GM垂直平分AD,
∴GD=GA=DA,
∴△ADG是等边三角形,
∴∠DAG=60°,
∴旋转角θ=60°;
②当点G在AD左侧时,如图2,同理可得△ADG是等边三角形,
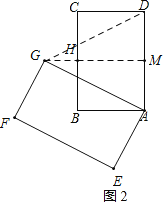
∴∠DAG=60°,
∴旋转角θ=360°﹣60°=300°.
综上,θ的度数为60°或300°;
(3)有两种情况:
①如图3,当BG=BC=13时,过G作GH⊥CD于H,交AB于M,
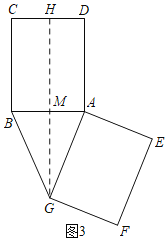
∵AG=BC=BG,
∴AM=BM=5,
Rt△AMG中,由勾股定理得:MG=![]() =
=![]() =12,
=12,
∵AB∥CD,
∴MH=BC=13,
∴GH=13+12=25,即点G到直线CD的距离是25;
②如图4,过G作MH⊥CD于H,交AB于M,
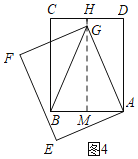
同理得GM=12,
∴GH=13﹣12=1,即点G到直线CD的距离是1;
综上,即点G到直线CD的距离是25或1.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】(感知)如图①,正方形![]() 中,点
中,点![]() 在
在![]() 边上,
边上,![]() 平分
平分![]() .若我们分别延长
.若我们分别延长![]() 与
与![]() ,交于点
,交于点![]() ,则易证
,则易证![]() .(不需要证明)
.(不需要证明)
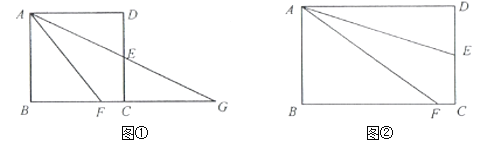
(探究)如图②,在矩形![]() 中,点
中,点![]() 在
在![]() 边的中点,点
边的中点,点![]() 在
在![]() 边上,
边上,![]() 平分
平分![]() .求证:
.求证:![]() .
.
(应用)在(探究)的条件下,若![]() ,
,![]() ,直接写出
,直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知,抛物线![]() (a
(a![]() 0)的顶点为A(s,t)(其中s
0)的顶点为A(s,t)(其中s![]() 0) .
0) .
(1)若抛物线经过(2,2)和(-3,37)两点,且s=3.
①求抛物线的解析式;
②若n>3, 设点M(![]() ),N(
),N(![]() )在抛物线上,比较
)在抛物线上,比较![]() ,
,![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
(2)若a=2,c=-2,直线![]() 与抛物线
与抛物线![]() 的交于点P和点Q,点P的横坐标为h,点Q的横坐标为h+3,求出b和h的函数关系式;
的交于点P和点Q,点P的横坐标为h,点Q的横坐标为h+3,求出b和h的函数关系式;
(3)若点A在抛物线![]() 上,且2≤s<3时,求a的取值范围.
上,且2≤s<3时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人要某风景区游玩,每天某一时段开往该景区有三辆汽车(票价相同),但是他们不清楚这三辆车的舒适程度,也不知道汽车开来的顺序,两人采用了不同的乘车方案:
甲无论如何总是上开来的第一辆车,而乙则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车辆的舒适状况,如果第二辆车状况比第一辆好,他就上第二辆车,如果第二辆不比第一辆好,他就上第三辆车.这三辆车的舒适程度为上、中、下三等,请解决下面的问题:
(1)请用画树形图或列表的方法分析这三辆车出现的先后顺序,写出所有可能的结果;(用上中下表示)
(2)分析甲、乙两人采用的方案,谁的方案使自己坐上上等车的可能性大,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
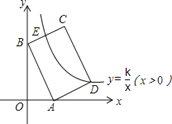
【题目】如图,在平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=![]() (x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为__.
(x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决问题.
学校要购买A,B两种型号的足球,按体育器材门市足球销售价格(单价)计算:若买2个A型足球和3个B型足球,则要花费370元,若买3个A型足球和1个B型足球,则要花费240元.
(1)求A,B两种型号足球的销售价格各是多少元/个?
(2)学校拟向该体育器材门市购买A,B两种型号的足球共20个,且费用不低于1300元,不超过1500元,则有哪几种购球方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段OA=2,OP=1,将线段OP绕点O任意旋转时,线段AP的长度也随之改变,则下列结论:
①AP的最小值是1,最大值是4;
②当AP=2时,△APO是等腰三角形;
③当AP=1时,△APO是等腰三角形;
④当AP=![]() 时,△APO是直角三角形;
时,△APO是直角三角形;
⑤当AP=![]() 时,△APO是直角三角形.
时,△APO是直角三角形.
其中正确的是( )
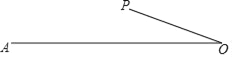
A. ①④⑤ B. ②③⑤ C. ②④⑤ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆朝天门码头位于置庆市油中半岛的嘉陵江与长江交汇处,是重庆最古老的码头.如图,小王在码头某点E处测得朝天门广场上的某高楼AB的顶端A的仰角为45°,接着他沿着坡度为1:2.4的斜坡EC走了26米到达坡顶C处,到C处后继续朝高楼AB的方向前行16米到D处,在D处测得A的仰角为74°,则此时小王距高楼的距离BD的为( )米(结果精确到1米,参考数据:sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
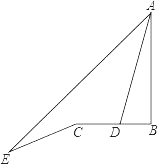
A.12B.13C.15D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C = 90°,点O是斜边AB上一定点,到点O的距离等于OB的所有点组成图形W,图形W与AB,BC分别交于点D,E,连接AE,DE,∠AED=∠B.

(1)判断图形W与AE所在直线的公共点个数,并证明.
(2)若![]() ,
,![]() ,求OB.
,求OB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com