
����Ŀ���ס�������Ҫij�羰�����棬ÿ��ijһʱ�ο����þ���������������Ʊ����ͬ�����������Dz�����������������ʳ̶ȣ�Ҳ��֪������������˳�����˲����˲�ͬ�ij˳�������
��������������Ͽ����ĵ�һ���������������ȹ۲���ϳ�������һ��������ʱ�������ϳ���������ϸ�۲쳵��������״��������ڶ�����״���ȵ�һ���ã������ϵڶ�����������ڶ������ȵ�һ���ã������ϵ����������������������ʳ̶�Ϊ�ϡ��С������ȣ�������������⣺
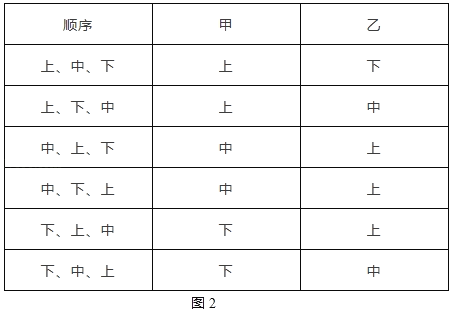
��1�����û�����ͼ���б��ķ������������������ֵ��Ⱥ�˳��д�����п��ܵĽ�������������±�ʾ��
��2�������ס������˲��õķ�����˭�ķ���ʹ�Լ������ϵȳ��Ŀ����Դ�˵�����ɣ�
���𰸡���1������6�֣��������£����������У����������£����������ϣ����������У����������ϣ�����2���������ϵȳ��Ŀ����Դ�
��������
��1�������б��ķ����ó�����6�ֿ��ܵĽ����
��2�������б���չʾ���ҳ˳������н����Ȼ��������dz����ϵȳ��ĸ��ʣ��ٱȽϸ��ʵĴ�С��
��1���������������Ⱥ�˳���б���ͼ1��ʾ��
���п��ܵĽ����6�֣�
��2���б���ͼ2��ʾ��
�������ϵȳ��ĸ���=![]() ��
��
�������ϵȳ��ĸ���=![]() =
=![]() ��
��
�����������ϵȳ��Ŀ����Դ�




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�������������¶��壺���ں���![]() ������
������![]() ������ֵ
������ֵ![]() ����
����![]() ��������
��������![]() ����ƴ˺���Ϊ��
����ƴ˺���Ϊ��![]() ���ͺϺ�������
���ͺϺ�������
���磺����������![]() ����
����![]() ʱ��
ʱ��![]() ����
����![]() ����ã�
����ã�![]() �����Ժ���
�����Ժ���![]() Ϊ��3���ͺϺ�������
Ϊ��3���ͺϺ�������
��1����һ�κ���![]() Ϊ��1���ͺϺ���������
Ϊ��1���ͺϺ���������![]() ��ֵ_________��
��ֵ_________��
��2����֪���κ���![]() ����
����![]() ʱ��
ʱ��![]() �ǡ�
�ǡ�![]() ���ͺϺ���������
���ͺϺ���������![]() ��ȡֵ��Χ_________��
��ȡֵ��Χ_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ij��ѧѧ�������������ϲ���������顢������������ӡ����ʵ���ĸ�������������е���ͳ�ƣ��ִӸ�У�����ȡ![]() ��ѧ����Ϊ�����������ʾ�����ķ�ʽ�ռ�����(�����ʾ������ÿ��ѧ��ֻ��ѡ������--��)�����ݵ���õ������ݻ��Ƴ�����ͼ��ʾ��������������ͳ��ͼ����ͼ���ṩ����Ϣ������������⣺
��ѧ����Ϊ�����������ʾ�����ķ�ʽ�ռ�����(�����ʾ������ÿ��ѧ��ֻ��ѡ������--��)�����ݵ���õ������ݻ��Ƴ�����ͼ��ʾ��������������ͳ��ͼ����ͼ���ṩ����Ϣ������������⣺
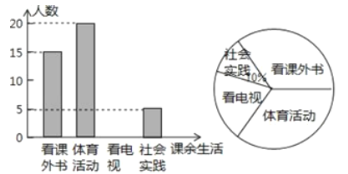
��1��![]() ��ֱ�Ӳ�ȫ����ͳ��ͼ��
��ֱ�Ӳ�ȫ����ͳ��ͼ��
��2������У����ѧ��![]() �����Թ��Ƹ�Уϲ�����������ѧ��������
�����Թ��Ƹ�Уϲ�����������ѧ��������
��3����������ϲ���������![]() ��ѧ������
��ѧ������![]() ��������
��������![]() ��Ů�����ִ���
��Ů�����ִ���![]() ��ѧ���������ȡ
��ѧ���������ȡ![]() ���������б�����״ͼ�ķ�����ǡ�ó鵽
���������б�����״ͼ�ķ�����ǡ�ó鵽![]() �������ĸ��ʣ�
�������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
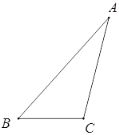
����Ŀ��������С����Ƶ����������εĸ������ij߹���ͼ����.
��֪����ABC��
������BC���ϵĸ��ߣ�
��������ͼ��
���Ե�CΪԲ�ģ�CAΪ�뾶������
���Ե�BΪԲ�ģ�BAΪ�뾶�����������ཻ�ڵ�D��
������AD����BC���ӳ����ڵ�E��
�����߶�AE������������BC���ϵĸ��ߣ�
����С����Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ���������ͼ�ۼ���
��2���������֤��.
֤������CA=CD��
���C���߶�AD�Ĵ�ֱƽ�����ϣ� �� �������������ݣ���
�� = ��
���B���߶�AD�Ĵ�ֱƽ�����ϣ�
�� BC���߶�AD�Ĵ�ֱƽ����.
��AD��BC��
��AE����BC���ϵĸ��ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��ͼ����
��ͼ����![]() �ύ��
�ύ��![]() ��
��![]() ���㣨��
���㣨��![]() �ڵ�
�ڵ�![]() ����ߣ�����
����ߣ�����![]() Ϊ�����ߵĶ��㣮
Ϊ�����ߵĶ��㣮
��1���������ߵĺ�������ʽ��
��2�������˶��κ����Ĵ���ͼ��
��3����![]() Ϊ�߶�
Ϊ�߶�![]() ��һ�㣨��
��һ�㣨��![]() �����
�����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ��
��![]() ��Ĵ��ߣ��������߽��ڵ�
��Ĵ��ߣ��������߽��ڵ�![]() ������
������![]() ��
��![]() ���������ڵ�
���������ڵ�![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() �ڵ�
�ڵ�![]() ��ߣ�����
��ߣ�����![]() ���ܳ����ʱ��
���ܳ����ʱ��![]() �ĺ����꣮
�ĺ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
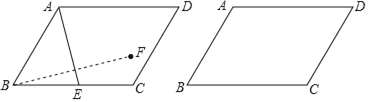
����Ŀ����ͼ����֪ABCD�У���ABC��60����AB��4��BC��m��EΪBC���ϵĶ��㣬����AE������B����ֱ��AE�ĶԳƵ�F��
��1����m��6���ٵ���Fǡ�����ڡ�BCD��ƽ������ʱ����BE�ij���
�ڵ�E��C�غ�ʱ�����F��ֱ��BC�ľ��룻
��2������F��ֱ��BC�ľ���d����������2![]() ��2��d��2
��2��d��2![]() +4����m��ȡֵ��Χ��
+4����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�Ƶ�A˳ʱ����ת����0��ܦȡ�360�������õ�����AEFG��
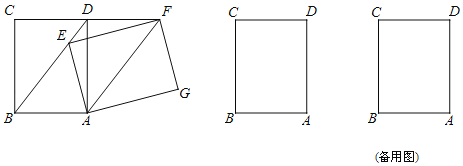
��1������E��BD��ʱ����֤��AF��BD��
��2����GC��GBʱ��������
��3����AB��10��BG��BC��13ʱ�����G��ֱ��CD�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ҫ���첿��ũ����ֲ�߲�.�����飬ƽ��ÿĶ���������![]() Ԫ�����ӵι��豸�ȷ��ã�Ԫ����������
Ԫ�����ӵι��豸�ȷ��ã�Ԫ����������![]() ��Ķ����ƽ�ֳ����ȣ�����ϵ��Ϊ
��Ķ����ƽ�ֳ����ȣ�����ϵ��Ϊ![]() �������������
�������������![]() ���ڲ���Ҫ���ӣ�ÿĶ��ֲ�߲˻������ӡ��˹�����
���ڲ���Ҫ���ӣ�ÿĶ��ֲ�߲˻������ӡ��˹�����![]() Ԫ���������ÿ����迪֧�������
Ԫ���������ÿ����迪֧�������![]() Ķ��ÿĶ�߲�������۽��Ϊ
Ķ��ÿĶ�߲�������۽��Ϊ![]() Ԫ�������������⣬û���������ã�
Ԫ�������������⣬û���������ã�
��1���赱������Ϊ![]() Ԫ����
Ԫ����![]() ��
��![]() �ĺ�����ϵʽ���ú�
�ĺ�����ϵʽ���ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��2����![]() �������
�������![]() ����㣬�Ƿ�������Խ������Խ�������Ϊ����ʱ���Եõ�������棿
����㣬�Ƿ�������Խ������Խ�������Ϊ����ʱ���Եõ�������棿
��3����![]() ʱ����
ʱ����![]() ����㣬��ȷ����������Խ������ҲԽ����
����㣬��ȷ����������Խ������ҲԽ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
ע������=���۽��-�������+�ι��豸�ȷ�+���ӡ��˹��ѣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��ж����������������������أ����������ѿ̲��ݻ�������ij�����̳��������ڽ�����Ҫ����������ij�ּ��ÿ������������������200Ԫ/̨�������г����ۺ��֣���һ�����ڣ����ۼ���400Ԫ/̨ʱ�����۳�200̨�����ۼ�ÿ����10Ԫ���Ϳɶ��۳�50̨���������̹涨���ֿ����������ۼ۲��ܵ���300Ԫ/̨������������ÿ��Ҫ��ɲ�����450̨����������
��1����ȷ����������y��̨�����ۼ�x��Ԫ/̨��֮��ĺ�����ϵʽ��������Ա���x��ȡֵ��Χ��
��2�����ۼ�x��Ԫ/̨����Ϊ����ʱ���̳�ÿ���������ֿ�������������õ�����w��Ԫ�������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com