
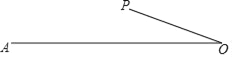
【题目】如图,线段OA=2,OP=1,将线段OP绕点O任意旋转时,线段AP的长度也随之改变,则下列结论:
①AP的最小值是1,最大值是4;
②当AP=2时,△APO是等腰三角形;
③当AP=1时,△APO是等腰三角形;
④当AP=![]() 时,△APO是直角三角形;
时,△APO是直角三角形;
⑤当AP=![]() 时,△APO是直角三角形.
时,△APO是直角三角形.
其中正确的是( )
A. ①④⑤ B. ②③⑤ C. ②④⑤ D. ③④⑤
【答案】C
【解析】
①根据题意求出AP的最小值和最大值是,判断即可;
②根据等腰三角形的定义得到△APO是等腰三角形;
③根据三角形的三边关系得到△APO不存在;
④根据勾股定理的逆定理计算,得到△APO是直角三角形;
⑤根据勾股定理的逆定理计算,得到△APO是直角三角形.
①当点P在线段OA上时,AP最小,最小值为2-1=1,
当点P在线段AO的延长线上时,AP最大,最大值为2+1=3,①错误;
②当AP=2时,AP=AO,
则△APO是等腰三角形,②正确;
③当AP=1时,AP+OP=OA,△AOP不存在,
△APO是等腰三角形错误,③错误;
④当AP=![]() 时,AP2+OP2=3+1=4,OA2=4,
时,AP2+OP2=3+1=4,OA2=4,
∴AP2+OP2=OA2,
∴△APO是直角三角形,④正确;
⑤当AP=![]() 时,AP2=5,OP2+OA2=1+4=5,
时,AP2=5,OP2+OA2=1+4=5,
∴AO2+OP2=PA2,
∴△APO是直角三角形,⑤正确,
故选C.


科目:初中数学 来源: 题型:
【题目】某汽车在刹车后行驶的距离s(单位:米)与时间t(单位:秒)之间的关系得部分数据如下表:
时间t(秒) | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | … |
行驶距离s(米) | 0 | 2.8 | 5.2 | 7.2 | 8.8 | 10 | 10.8 | … |
假设这种变化规律一直延续到汽车停止.
(1)根据这些数据在给出的坐标系中画出相应的点;
(2)选择适当的函数表示s与t之间的关系,求出相应的函数解析式;
(3)①刹车后汽车行驶了多长距离才停止? ②当t分别为t1 , t2(t1<t2)时,对应s的值分别为s1 , s2 , 请比较 ![]() 与
与 ![]() 的大小,并解释比较结果的实际意义.
的大小,并解释比较结果的实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:______________;结论:________.(均填写序号)
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
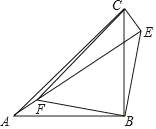
【题目】如图,点E是等腰三角形纸片ABC外一点,∠ABC=90°,连接AE,点F是线段AE(不与点A,E重合)上一点,在△EBF中,EB=FB,∠EBF=90°,连接CE,CF
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,初三一班数学兴趣小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°.朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度为1: ![]() (即AB:BC=1:
(即AB:BC=1: ![]() ),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
在公式(a+1)2=a2+2a+1中,当a分别取1,2,3,4,…,n时,可得以下等式:
(1+1)2=12+2×1+1;
(2+1)2=22+2×2+1;
(3+1)2=32+2×3+1;
(4+1)2=42+2×4+1;
……
(n+1)2=n2+2n+1.
将这几个等式的左右两边分别相加,可以推导出求和公式:1+2+3+4+…+n=![]() .
.
请写出推导过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数 ![]() 的图像与反比例函数
的图像与反比例函数 ![]() (
( ![]() 为常数,且
为常数,且 ![]() )的图像都经过点
)的图像都经过点 ![]()

(1)求点 ![]() 的坐标及反比例函数的表达式;
的坐标及反比例函数的表达式;
(2)结合图像直接比较:当 ![]() 时,
时, ![]() 和
和 ![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com