
【题目】在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:______________;结论:________.(均填写序号)
证明:
【答案】题设:①②③;结论:④,证明见解析
【解析】
解题设:①②③;结论:④.
证明:∵BF=EC,∴BF+CF=EC+CF,即BC=EF。
在△ABC和△DEF中,AB=DE,∠B=∠E,BC=EF,
∴△ABC≌△DEF(SAS),∴∠1=∠2。
此题可以分成三种情况:
情况一:题设:①②③;结论:④,可以利用SAS定理证明△ABC≌△DEF。
情况二:题设:①③④;结论:②,可以利用AAS证明△ABC≌△DEF:
在△ABC和△DEF中,∵ AB=DE,∠B=∠E,∠1=∠2,∴△ABC≌△DEF(AAS)。
∴BC=EF,∴BC-FC=EF-FC,即BF=EC。
情况三:题设:②③④;结论:①,可以利用ASA证明△ABC≌△DEF,再根据全等三角形的
性质可推出结论:
∵BF=EC,∴BF+CF=EC+CF,即BC=EF。
在△ABC和△DEF中,∵∠B=∠E ,BC=EF,∠1=∠2,∴△ABC≌△DEF(ASA)。∴AB=DE。


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】下面四个整式中,不能表示图中阴影部分面积的是( )

A. (x+3)(x+2)﹣2x B. x(x+3)+6 C. 3(x+2)+x2 D. x2+5x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,射线OC在∠A0B的内部,图中共有3个角:∠AOB、∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“定分线”
(1)一个角的平分线______这个角的“定分线”;(填“是”或“不是”)
(2)如图2,若∠MPN=![]() ,且射线PQ是∠MPN的“定分线”,则∠MPQ=_____(用含a的代数式表示出所有可能的结果)
,且射线PQ是∠MPN的“定分线”,则∠MPQ=_____(用含a的代数式表示出所有可能的结果)
(3)如图2,若∠MPN=45°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成90°时停止旋转,旋转的时间为t秒.同时射线PM绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止.当PQ是∠MPN的“定分线”时,求t的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一副直角三角尺的顶点叠一起放在点A处,∠BAC=60°,∠DAE=45°,保持三角尺ABC不动,三角尺AED绕点A顺时针旋转,旋转角度小于180°.
(1)如图2,AD是∠EAC的角平分线,直接写出∠DAB的度数;
(2)在旋转的过程中,当∠EAB和∠DAC互余时,求∠BAD的值.
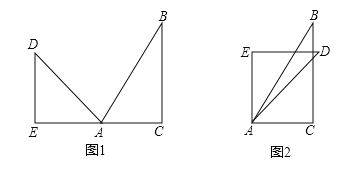
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段OA=2,OP=1,将线段OP绕点O任意旋转时,线段AP的长度也随之改变,则下列结论:
①AP的最小值是1,最大值是4;
②当AP=2时,△APO是等腰三角形;
③当AP=1时,△APO是等腰三角形;
④当AP=![]() 时,△APO是直角三角形;
时,△APO是直角三角形;
⑤当AP=![]() 时,△APO是直角三角形.
时,△APO是直角三角形.
其中正确的是( )
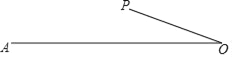
A. ①④⑤ B. ②③⑤ C. ②④⑤ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆车长为4米的小轿车和一辆车长为20米的大货车,在长为1200米隧道的两个入口同时开始相向而行,小轿车的速度是大货车速度的3倍,大货车速度为10米/秒.
(1)求两车相遇的时间;
(2)求两车从相遇到完全离开所需的时间;
(3)当小轿车车头和大货车车头相遇后,求小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时所需的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小石和小丁利用盒子里的三张卡片做游戏,卡片上分别写有![]() ,
,![]() ,
,![]() ,这些卡片除了字母外完全相同.从中随机摸出一张卡片记下字母,放回盒子后充分搅匀,再从中随机 摸出一张卡片记下字母.如果两次摸到的卡片字母相同则小石获胜,否则小丁获胜,这个游戏公平吗?请用画树状图或列表的方法说明理由.
,这些卡片除了字母外完全相同.从中随机摸出一张卡片记下字母,放回盒子后充分搅匀,再从中随机 摸出一张卡片记下字母.如果两次摸到的卡片字母相同则小石获胜,否则小丁获胜,这个游戏公平吗?请用画树状图或列表的方法说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com