
【题目】一辆车长为4米的小轿车和一辆车长为20米的大货车,在长为1200米隧道的两个入口同时开始相向而行,小轿车的速度是大货车速度的3倍,大货车速度为10米/秒.
(1)求两车相遇的时间;
(2)求两车从相遇到完全离开所需的时间;
(3)当小轿车车头和大货车车头相遇后,求小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时所需的时间.
【答案】(1)30秒;(2)0.6秒;(3)![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)设两车经过x秒相遇,根据相遇时,两车行驶的路程之和等于隧道的长列出方程,解方程即可;
(2)设两车从相遇到完全离开所需的时间为y秒,等量关系为:速度和×时间=两车的车长之和,依此列出方程,解方程即可;
(3)先根据小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍,求出两车相遇后一共行驶的路程之和,再除以速度和即可.分两种情况进行讨论:①车尾相遇前;②车尾相遇后.
(1)设两车经过x秒相遇,根据题意得:
(10+30)x=1200
解得:x=30.
答:两车经过30秒相遇;
(2)设两车从相遇到完全离开所需的时间为y秒,根据题意得:
(10+30)y=4+20
解得:y=0.6.
答:两车从相遇到完全离开所需的时间为0.6秒;
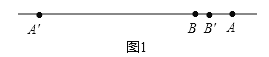
(3)设AB表示车长为4米的小轿车,其中点A表示车头,点B表示车尾,A'B'表示车长为20米的大货车,其中点A'表示车头,点B'表示车尾,则AB=4米,A'B'=20米,设BB'=a米.
分两种情况:①车尾相遇前,如图1,则AB'=(4﹣a)米.
小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时,AA'=4BB',所以20+4﹣a=4a,解得:a![]() ,则AA'
,则AA'![]() ,故所求时间为:
,故所求时间为:![]() (10+30)
(10+30)![]() (秒);
(秒);
②车尾相遇后,如图2,则AB'=(4+a)米.
小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时,AA'=4BB',所以20+4+a=4a,解得:a=8,则AA'=32,故所求时间为:32÷(10+30)![]() (秒).
(秒).

综上所述:当小轿车车头和大货车车头相遇后,小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时所需的时间为![]() 秒或
秒或![]() 秒.
秒.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E、F分别在BC、CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处.则BC:AB的值为 . 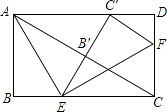
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威丽商场销售A,B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1 100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元;
(2)由于需求量大,A,B两种商品很快售完,威丽商场决定再一次购进A,B两种商品共34件.如果将这34件商品全部售完后所得利润不低于4 000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:______________;结论:________.(均填写序号)
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,初三一班数学兴趣小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°.朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度为1: ![]() (即AB:BC=1:
(即AB:BC=1: ![]() ),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,点M,N在射线OA上(都不与点O重合),且MN=2,点P在射线OB上,若△MPN为等腰直角三角形,则PO的长为 ___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知ABCD的一组邻边AB、AD的长是关于x的方程x2﹣4x+m=0的两个实根.
(1)当m为何值时,四边形ABCD是菱形?
(2)在第(1)问的前提下,若∠ABC=60°,求ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8)、动点M、N分别从O、B同时出发,都以每秒1个单位的速度运动、其中,点M沿OA向终点A运动,点N沿BC向终点C运动、过点N作NP⊥BC,交AC于P,连结MP、已知动点运动了t秒、
(1)P点的坐标为( , )(用含t的代数式表示);
(2)试求 △MPA面积的最大值,并求此时t的值;
(3)请你探索:当t为何值时,△MPA是一个等腰三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com