
【题目】已知ABCD的一组邻边AB、AD的长是关于x的方程x2﹣4x+m=0的两个实根.
(1)当m为何值时,四边形ABCD是菱形?
(2)在第(1)问的前提下,若∠ABC=60°,求ABCD的面积.
【答案】
(1)解:四边形ABCD是菱形时,AB=AD,
∵AB,AD的长是关于x的方程x2﹣mx+4=0的两个实数根,
∴△=(﹣4)2﹣4m=0,
解得:m=4,
∴当m=4时,四边形ABCD是菱形
(2)解:如图,连接AC、BD交于点O,

当m=4时,
x2﹣4x+4=0,
解得:x1=x2=2,
则AB=2,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠ABO= ![]() ∠ABC=30°,
∠ABC=30°,
DB═2OB,AC=2OA,AC⊥BD,
在直角△AOB中,
∵∠ABO=30°,
∴OA= ![]() AB=1,
AB=1,
0B= ![]() ,
,
BD=2OB=2 ![]() ,
,
AC=2OA=2,
∴S菱形ABCD= ![]() BDAC=
BDAC= ![]() ×2×2
×2×2 ![]() =2
=2 ![]() .
.
【解析】(1)由菱形的判定知四边形ABCD是菱形时,AB=AD,根据方程根的判别式知△=(﹣4)2﹣4m=0,解方程求出m的值,从而得出结论;
(2)连接AC、BD交于点O,首先计算出菱形的边长AB,然后根据菱形的对角线垂直、平分、每条对角线平分一组对角,得出∠ABO=30°,DB═2OB,AC=2OA,AC⊥BD,在直角△AOB中,利用含30![]() 角的直角三角形的边之间的关系求出OA,OB,进而得出BD,AC,根据菱形的面积等于两对角线之积的一半得出答案。
角的直角三角形的边之间的关系求出OA,OB,进而得出BD,AC,根据菱形的面积等于两对角线之积的一半得出答案。
【考点精析】掌握求根公式是解答本题的根本,需要知道根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.


科目:初中数学 来源: 题型:
【题目】下面四个整式中,不能表示图中阴影部分面积的是( )

A. (x+3)(x+2)﹣2x B. x(x+3)+6 C. 3(x+2)+x2 D. x2+5x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆车长为4米的小轿车和一辆车长为20米的大货车,在长为1200米隧道的两个入口同时开始相向而行,小轿车的速度是大货车速度的3倍,大货车速度为10米/秒.
(1)求两车相遇的时间;
(2)求两车从相遇到完全离开所需的时间;
(3)当小轿车车头和大货车车头相遇后,求小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时所需的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】布袋中有红、黄、蓝三种不同颜色的球各一个,从中先摸出一个球,记录下颜色后不放回布袋,将布袋搅匀,再摸出一个球,这时摸出的两个球是“一红一黄”的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的图象反映的过程是:小强星期天从家跑步去体育场,在那里锻炼了一会儿后又走到文具店去买笔,然后步行回家,其中x表示时间,y表示小强离家的距离,根据图象回答下列问题.
(1)体育场离小强家有多远?小强从家到体育场用了多长时间?
(2)体育场距文具店多远?
(3)小强在文具店逗留了多长时间?
(4)小强从文具店回家的平均速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
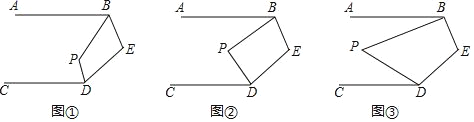
【题目】已知AB∥CD,解决下列问题:
(1)如图①,BP、DP分别平分∠ABE、∠CDE,若∠E=100°,求∠P的度数.
(2)如图②,若∠ABP=![]() ∠ABE,∠CDP=
∠ABE,∠CDP=![]() ∠CDE,试写出∠P与∠E的数量关系并说明理由.
∠CDE,试写出∠P与∠E的数量关系并说明理由.
(3)如图③,若∠ABP=![]() ∠ABE,∠CDP=
∠ABE,∠CDP=![]() ∠CDE,设∠E=m°,求∠P的度数(直接用含n、m的代数式表示,不需说明理由).
∠CDE,设∠E=m°,求∠P的度数(直接用含n、m的代数式表示,不需说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小石和小丁利用盒子里的三张卡片做游戏,卡片上分别写有![]() ,
,![]() ,
,![]() ,这些卡片除了字母外完全相同.从中随机摸出一张卡片记下字母,放回盒子后充分搅匀,再从中随机 摸出一张卡片记下字母.如果两次摸到的卡片字母相同则小石获胜,否则小丁获胜,这个游戏公平吗?请用画树状图或列表的方法说明理由.
,这些卡片除了字母外完全相同.从中随机摸出一张卡片记下字母,放回盒子后充分搅匀,再从中随机 摸出一张卡片记下字母.如果两次摸到的卡片字母相同则小石获胜,否则小丁获胜,这个游戏公平吗?请用画树状图或列表的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:
单价x(元/件) | 30 | 34 | 38 | 40 | 42 |
销量y(件) | 40 | 32 | 24 | 20 | 16 |
(1)通过对上面表格中的数据进行分析,发现销量 ![]() (件)与单价
(件)与单价 ![]() (元/件)之间存在一次函数关系,求
(元/件)之间存在一次函数关系,求 ![]() 关于
关于 ![]() 的函数关系式(不需要写出函数自变量的取值范围);
的函数关系式(不需要写出函数自变量的取值范围);
(2)预计在今后的销售中,销量与单价仍然存在(1)中的关系,且该产品的成本是20元/件.为使工厂获得最大利润,该产品的单价应定为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com