
【题目】威丽商场销售A,B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1 100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元;
(2)由于需求量大,A,B两种商品很快售完,威丽商场决定再一次购进A,B两种商品共34件.如果将这34件商品全部售完后所得利润不低于4 000元,那么威丽商场至少需购进多少件A种商品?
【答案】(1)每件A种商品售出后所得利润为200元,B种商品售出后所得利润为100元;(2)威丽商场至少需购进6件A种商品
【解析】
(1)设A种商品售出后所得利润为x元,B种商品售出后所得利润为y元.由售出1件A种商品和4件B种商品所得利润为600元,售出3件A种商品和5件B种商品所得利润为1100元建立两个方程,构成方程组求出其解就可以;
(2)设购进A种商品a件,则购进B种商品(34-a)件.根据获得的利润不低于4000元,建立不等式求出其解就可以了.
(1)设每件A种商品售出后所得利润为x元,每件B种商品售出后所得利润为y元,
由题意,得![]() ,
,
解得:![]() ,
,
答:每件A种商品售出后所得利润为200元,每件B种商品售出后所得利润为100元;
(2)设购进A种商品a件,则购进B种商品(34-a)件,
由题意,得200a+100(34-a)≥4000,
解得:a≥6
答:威丽商场至少需购进6件A种商品.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】已知:如图:∠1=∠2,∠3+∠4= 180°;确定直线a,c的位置关系,并说明理由;
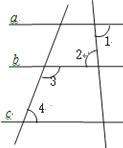
解:a c;
理由:∵∠1=∠2( ),
∴ a // ( );
∵ ∠3+∠4= 180°( ),
∴ c // ( );
∵ a // ,c // ,
∴ // ( );
查看答案和解析>>
科目:初中数学 来源: 题型:
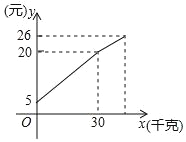
【题目】王大爷带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价出售一些后,又降价出售,售出土豆的千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示.根据图象回答下列问题:
(1)王大爷自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
(4)写出售出土豆的千克数x与他手中持有的钱数y(含备用零钱)的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面四个整式中,不能表示图中阴影部分面积的是( )

A. (x+3)(x+2)﹣2x B. x(x+3)+6 C. 3(x+2)+x2 D. x2+5x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,射线OC在∠A0B的内部,图中共有3个角:∠AOB、∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“定分线”
(1)一个角的平分线______这个角的“定分线”;(填“是”或“不是”)
(2)如图2,若∠MPN=![]() ,且射线PQ是∠MPN的“定分线”,则∠MPQ=_____(用含a的代数式表示出所有可能的结果)
,且射线PQ是∠MPN的“定分线”,则∠MPQ=_____(用含a的代数式表示出所有可能的结果)
(3)如图2,若∠MPN=45°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成90°时停止旋转,旋转的时间为t秒.同时射线PM绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止.当PQ是∠MPN的“定分线”时,求t的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一副直角三角尺的顶点叠一起放在点A处,∠BAC=60°,∠DAE=45°,保持三角尺ABC不动,三角尺AED绕点A顺时针旋转,旋转角度小于180°.
(1)如图2,AD是∠EAC的角平分线,直接写出∠DAB的度数;
(2)在旋转的过程中,当∠EAB和∠DAC互余时,求∠BAD的值.
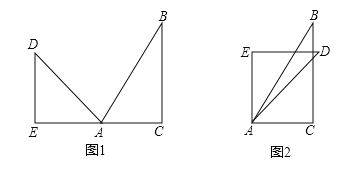
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆车长为4米的小轿车和一辆车长为20米的大货车,在长为1200米隧道的两个入口同时开始相向而行,小轿车的速度是大货车速度的3倍,大货车速度为10米/秒.
(1)求两车相遇的时间;
(2)求两车从相遇到完全离开所需的时间;
(3)当小轿车车头和大货车车头相遇后,求小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时所需的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
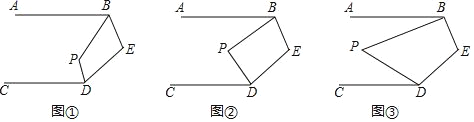
【题目】已知AB∥CD,解决下列问题:
(1)如图①,BP、DP分别平分∠ABE、∠CDE,若∠E=100°,求∠P的度数.
(2)如图②,若∠ABP=![]() ∠ABE,∠CDP=
∠ABE,∠CDP=![]() ∠CDE,试写出∠P与∠E的数量关系并说明理由.
∠CDE,试写出∠P与∠E的数量关系并说明理由.
(3)如图③,若∠ABP=![]() ∠ABE,∠CDP=
∠ABE,∠CDP=![]() ∠CDE,设∠E=m°,求∠P的度数(直接用含n、m的代数式表示,不需说明理由).
∠CDE,设∠E=m°,求∠P的度数(直接用含n、m的代数式表示,不需说明理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com