
【题目】如图1,将一副直角三角尺的顶点叠一起放在点A处,∠BAC=60°,∠DAE=45°,保持三角尺ABC不动,三角尺AED绕点A顺时针旋转,旋转角度小于180°.
(1)如图2,AD是∠EAC的角平分线,直接写出∠DAB的度数;
(2)在旋转的过程中,当∠EAB和∠DAC互余时,求∠BAD的值.
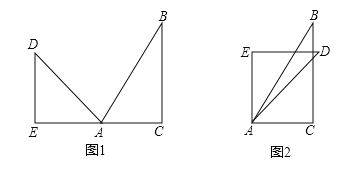
【答案】(1)15°;(2)∠BAD的值为7.5°或97.5°.
【解析】
(1)依据AD是∠EAC的角平分线,即可得出∠DAE=∠CAD=45°,再根据∠BAC=60°,即可得到∠DAB的度数;
(2)分两种情况讨论,设∠BAD=α,依据∠EAB和∠DAC互余,列方程求解即可.
(1)∵AD是∠EAC的角平分线,∴∠DAE=∠CAD=45°.
∵∠BAC=60°,∴∠DAB=60°﹣45°=15°;
(2)分两种情况讨论:
①如图1,当∠EAB和∠DAC互余时,设∠BAD=α,则∠BAE=45°﹣α,∠CAD=60°﹣α,∴45°﹣α+60°﹣α=90°,解得:α=7.5°;
②如图2,当∠EAB和∠DAC互余时,设∠BAD=α,则∠BAE=α﹣45°,∠CAD=α﹣60°,∴α﹣45°+α﹣60°=90°,解得:α=97.5°.

综上所述:当∠EAB和∠DAC互余时,∠BAD的值为7.5°或97.5°.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】某海滨浴场东西走向的海岸线可近似看作直线l(如图).救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号.他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙.乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东35°方向,甲、乙的游泳速度都是2米/秒.问谁先到达B处?请说明理由.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB的边OA上的一点:
(1)过点P画OB的垂线,垂足为H;
(2)过点H画OA的垂线,交OA于点C;
(3)再看画好垂线的图,你发现了哪个点到哪条直线的距离?分别量一量之后写出来.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威丽商场销售A,B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1 100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元;
(2)由于需求量大,A,B两种商品很快售完,威丽商场决定再一次购进A,B两种商品共34件.如果将这34件商品全部售完后所得利润不低于4 000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E.下列结论错误的是( )
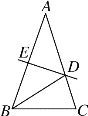
A. BD平分∠ABC B. △BCD的周长等于AB+BC
C. AD=BD=BC D. 点D是线段AC的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:______________;结论:________.(均填写序号)
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,点M,N在射线OA上(都不与点O重合),且MN=2,点P在射线OB上,若△MPN为等腰直角三角形,则PO的长为 ___.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com