
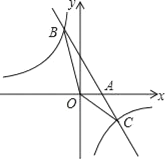
【题目】如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=![]() 相交于B(﹣1,5),C(
相交于B(﹣1,5),C(![]() ,d)两点.
,d)两点.
(1)利用图中条件,求反比例和一次函数的解析式;
(2)连接OB,OC,求△BOC的面积.
【答案】(1)反比例函数解析式为y=﹣![]() ,一次函数y1=﹣2x+3;(2)S△BOC=
,一次函数y1=﹣2x+3;(2)S△BOC=![]()
【解析】
(1)将点B的坐标代入反比例函数解析式求出c,从而得解,再将点C的坐标代入反比例函数解析式求出d,从而得到点C的坐标,然后利用待定系数法求一次函数解析式求解;
(2)根据一次函数解析式求出点A的坐标,再根据S△BOC=S△AOB+S△AOC列式计算即可得解.
解:(1)将B(﹣1,5)代入y2=![]() 得,
得, ![]() =5,
=5,
解得c=﹣5,
所以,反比例函数解析式为y=﹣![]() ,
,
将点C(![]() ,d)代入y=﹣
,d)代入y=﹣![]() 得d=﹣
得d=﹣![]() =﹣2,
=﹣2,
所以,点C的坐标为(![]() ,﹣2),
,﹣2),
将点B(﹣1,5),C(![]() ,﹣2)代入一次函数y1=kx+b得,
,﹣2)代入一次函数y1=kx+b得,
 ,
,
解得![]() ,
,
所以,一次函数y1=﹣2x+3;
(2)令y=0,则﹣2x+3=0,
解得x=![]() ,
,
所以,点A的坐标为(![]() ,0),
,0),
所以,OA=![]() ,
,
S△BOC=S△AOB+S△AOC,
=![]() ×
×![]() ×5+
×5+![]() ×
×![]() ×2,
×2,
=![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
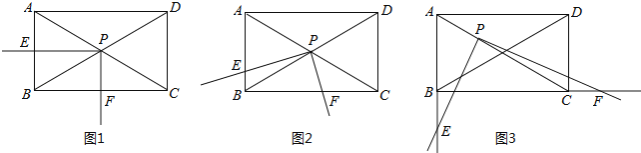
(1)当PE⊥AB,PF⊥BC时,如图1,则![]() 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求![]() 的值;
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3,![]() 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 和点
和点![]() 是反比例函数
是反比例函数![]() 图象上的两点,一次函数
图象上的两点,一次函数![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() .已知
.已知![]() 与
与![]() 的面积满足
的面积满足![]() .
.

(1)![]() = _____,
= _____,![]() = _____;
= _____;
(2)已知点![]() 在线段
在线段![]() 上,当
上,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了满足师生的阅读需求,某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.
(1)求这两年藏书的年均增长率;
(2)经统计知:中外古典名著的册数在2016年底仅占当时藏书总量的5.6%,在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书的年均增长率,那么到2018年底中外古典名著的册数占藏书总量的百分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点
经过点![]() 和点
和点![]() .
.
![]() 求该抛物线所对应的函数解析式;
求该抛物线所对应的函数解析式;
![]() 该抛物线与直线
该抛物线与直线![]() 相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线
相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线![]() 轴,分别与x轴和直线CD交于点M、N.
轴,分别与x轴和直线CD交于点M、N.
![]() 连结PC、PD,如图1,在点P运动过程中,
连结PC、PD,如图1,在点P运动过程中,![]() 的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;
的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;
![]() 连结PB,过点C作
连结PB,过点C作![]() ,垂足为点Q,如图2,是否存在点P,使得
,垂足为点Q,如图2,是否存在点P,使得![]() 与
与![]() 相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.
相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
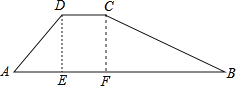
【题目】水库大坝截面的迎水坡坡比(DE与AE的长度之比)为1:0.6,背水坡坡比为1:2,大坝高DE=30米,坝顶宽CD=10米,求大坝的截面的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“每天锻炼一小时,健康生活一辈子”.为了选拔“阳光大课间”领操员,学校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
成绩/分 | 7 | 8 | 9 | 10 |
人数/人 | 2 | 5 | 4 | 4 |
(1)这组数据的众数是多少,中位数是多少.
(2)已知获得2018年四川省南充市的选手中,七、八、九年级分别有1人、2人、1人,学校准备从中随机抽取两人领操,求恰好抽到八年级两名领操员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线交于点O,DF∥AC,CF∥BD.

(1)求证:四边形OCFD是矩形;(2)若AD=5,BD=8,计算tan∠DCF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com