
【题目】抛物线![]() 经过点
经过点![]() 和点
和点![]() .
.
![]() 求该抛物线所对应的函数解析式;
求该抛物线所对应的函数解析式;
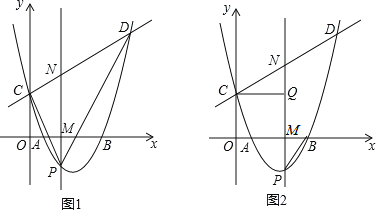
![]() 该抛物线与直线
该抛物线与直线![]() 相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线
相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线![]() 轴,分别与x轴和直线CD交于点M、N.
轴,分别与x轴和直线CD交于点M、N.
![]() 连结PC、PD,如图1,在点P运动过程中,
连结PC、PD,如图1,在点P运动过程中,![]() 的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;
的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;
![]() 连结PB,过点C作
连结PB,过点C作![]() ,垂足为点Q,如图2,是否存在点P,使得
,垂足为点Q,如图2,是否存在点P,使得![]() 与
与![]() 相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.
相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.

【答案】(1)![]() ;(2)在点P运动过程中,
;(2)在点P运动过程中,![]() 的面积存在最大值,最大值为81;
的面积存在最大值,最大值为81;
存在点P,使得![]() 与
与![]() 相似,点P的坐标为
相似,点P的坐标为![]() 或
或![]() .
.
【解析】
(1)由A、B两点的坐标,利用待定系数法可求得抛物线解析式;
(2)①联立抛物线与直线CD的解析式成方程组,通过解方程组可求出点C、D的坐标,设点P的坐标为![]() ,则点N的坐标为
,则点N的坐标为![]() ,
,![]() ,根据三角形面积公式可得出
,根据三角形面积公式可得出![]() ,利用二次函数的性质即可解决最值问题;②利用相似三角形的性质可得出:若
,利用二次函数的性质即可解决最值问题;②利用相似三角形的性质可得出:若![]() 与
与![]() 相似,则有
相似,则有![]() 或
或![]() ,设点P的坐标为
,设点P的坐标为![]() ,则点N的坐标为
,则点N的坐标为![]() ,点M的坐标为
,点M的坐标为![]() ,点Q的坐标为
,点Q的坐标为![]() ,进而可得出
,进而可得出![]() ,
,![]() ,
,![]() ,
,![]() ,将其代入
,将其代入![]() 或
或![]() 中即可求出x的值,结合
中即可求出x的值,结合![]() 即可得出点P的坐标.
即可得出点P的坐标.
(1)∵抛物线![]() 经过点
经过点![]() 和点
和点![]() ,
,
![]() ,
,
解得![]() ,
,
![]() 该抛物线对应的函数解析式为
该抛物线对应的函数解析式为![]() ;
;
(2))①联立抛物线与直线CD的解析式成方程组,
得:![]() ,
,
解得:![]() ,
,![]() ,
,
与![]() 相似,点P的坐标为
相似,点P的坐标为![]() 或
或![]() .
.
设点P的坐标为![]() ,则点N的坐标为
,则点N的坐标为![]() ,
,
![]() ,
,
 .
.
![]() ,
,
![]() 当
当![]() 时,
时,![]() 取最大值,最大值为81,
取最大值,最大值为81,
![]() 在点P运动过程中,
在点P运动过程中,![]() 的面积存在最大值,最大值为81.
的面积存在最大值,最大值为81.
②∵![]() ,
,
![]() 若
若![]() 与
与![]() 相似,则有
相似,则有![]() 或
或![]() ,
,
设点P的坐标为![]() ,则点N的坐标为
,则点N的坐标为![]() ,点M的坐标为
,点M的坐标为![]() ,点Q的坐标为
,点Q的坐标为![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
当![]() 或时,有
或时,有![]() ,
,
解得:![]() ,
,![]() 舍去
舍去![]() ,
,
![]() 点P的坐标为
点P的坐标为![]() ;
;
当![]() 时,有
时,有![]() ,
,
解得:![]() ,
,![]() 舍去
舍去![]() ,
,
![]() 点P的坐标为
点P的坐标为![]() .
.
综上所述:存在点P,使得![]() 与
与![]() 相似,点P的坐标为
相似,点P的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣2,3)、B(4,3)、C(﹣1,﹣3).

(1)求点C到x轴的距离;
(2)分别求△ABC的三边长;
(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同时抛掷A,B两个均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),设两立方体朝上的数字分别为x,y,并以此确定点P(x,y),那么点P落在直线y=-2x+9上的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AD是△ABC的角平分线,DF⊥AB,垂足为F,如图DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积( )

A.6B.12C.8D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于![]() 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(6+3m)x+(n-4).
(1)m为何值时,y随x的增大而减小.
(2)m,n分别为何值时,函数的图象经过原点?
(3)m,n分别为何值时,函数的图象与y=3x+2平行,且与y轴的交点在x轴的下方?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC的顶点坐标分别为A(﹣2,5),B(﹣4,3),C(﹣1,﹣1).

(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC关于y轴对称的△A2B2C2,并写出点A2的坐标;
(3)在边AC上有一点P(a、b),直接写出以上两次图形变换后的对称点P1、P2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com