
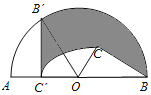
【题目】如图,C为半圆内一点,O为圆心,直径AB长为2cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为_____cm2.(结果保留π)
【答案】![]()
【解析】
根据已知条件和旋转的性质得出两个扇形的圆心角的度数,再根据扇形的面积公式进行计算即可得出答案.
解:∵∠BOC=60°,△B′OC′是△BOC绕圆心O逆时针旋转得到的,
∴∠B′OC′=60°,△BCO△B′C′O,
∴∠B′OC=60°,∠C′B′O=30°,
∴∠B′OB=120°,
∵AB=2cm,
∴OB=1cm,OC′=![]() ,
,
∴S扇形B′OB=![]() =
=![]() π,
π,
S扇形C′OC=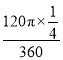 =
=![]() ,
,
∵阴影部分面积=S扇形B′OB+S△B′C′O﹣S△BCO﹣S扇形C′OC
∴阴影部分面积=S扇形B′OB+S△B′C′O﹣S△BCO﹣S扇形C′OC=S扇形B′OB﹣S扇形C′OC=![]() π﹣
π﹣![]() =
=![]() π;
π;
故答案为:![]() π.
π.


科目:初中数学 来源: 题型:
【题目】如图,点![]() 和点
和点![]() 是反比例函数
是反比例函数![]() 图象上的两点,一次函数
图象上的两点,一次函数![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() .已知
.已知![]() 与
与![]() 的面积满足
的面积满足![]() .
.

(1)![]() = _____,
= _____,![]() = _____;
= _____;
(2)已知点![]() 在线段
在线段![]() 上,当
上,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“每天锻炼一小时,健康生活一辈子”.为了选拔“阳光大课间”领操员,学校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
成绩/分 | 7 | 8 | 9 | 10 |
人数/人 | 2 | 5 | 4 | 4 |
(1)这组数据的众数是多少,中位数是多少.
(2)已知获得2018年四川省南充市的选手中,七、八、九年级分别有1人、2人、1人,学校准备从中随机抽取两人领操,求恰好抽到八年级两名领操员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线交于点O,DF∥AC,CF∥BD.

(1)求证:四边形OCFD是矩形;(2)若AD=5,BD=8,计算tan∠DCF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在点A,使得∠APC=30°,则称P为⊙C的半角关联点.
当⊙O的半径为1时,
(1)在点D(![]() ,﹣
,﹣![]() ),E(2,0),F(0,
),E(2,0),F(0,![]() )中,⊙O的半角关联点是 ;
)中,⊙O的半角关联点是 ;
(2)直线l:![]() 交x轴于点M,交y轴于点N,若直线l上的点P(m,n)是⊙O的半角关联点,求m的取值范围.
交x轴于点M,交y轴于点N,若直线l上的点P(m,n)是⊙O的半角关联点,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x﹣1)2过点(3,4),D为抛物线的顶点.
(1)求抛物线的解析式;
(2)若点B、C均在抛物线上,其中点B(0,1),且∠BDC=90°,求点C的坐标:
(3)如图,直线y=kx+1﹣k与抛物线交于P、Q两点,∠PDQ=90°,求△PDQ面积的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
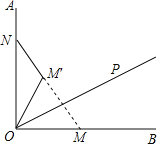
【题目】如图,∠AOB=90°,点P为∠AOB内部一点,作射线OP,点M在射线OB上,且OM=![]() ,点M′与点M关于射线OP对称,且直线MM′与射线OA交于点N.当△ONM'为等腰三角形时,ON的长为______.
,点M′与点M关于射线OP对称,且直线MM′与射线OA交于点N.当△ONM'为等腰三角形时,ON的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解下列方程,其中应在方程左右两边同时加上4的是( )
A. x2﹣2x=5 B. x2+4x=5 C. 2x2﹣4x=5 D. 4x2+4x=5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com