
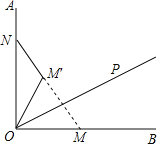
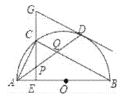
【题目】如图,∠AOB=90°,点P为∠AOB内部一点,作射线OP,点M在射线OB上,且OM=![]() ,点M′与点M关于射线OP对称,且直线MM′与射线OA交于点N.当△ONM'为等腰三角形时,ON的长为______.
,点M′与点M关于射线OP对称,且直线MM′与射线OA交于点N.当△ONM'为等腰三角形时,ON的长为______.
【答案】3或1
【解析】
如图分两种情况,Ⅰ.M'在∠AOB内部,Ⅱ.M'在∠AOB外部,由已知和等腰三角形性质、利用三角函数列方程,解直角三角形即可解答.
解:M'位置有两种情况,
Ⅰ.M'在∠AOB内部,如图1,
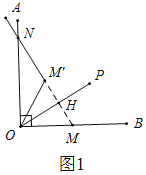
∵点M′与点M关于射线OP对称,△ONM'为等腰三角形,
∴M′N=OM′=OM=![]() ,MH=M′H,
,MH=M′H,
∵∵∠AOB=90°,cos∠OMN=![]()
∴![]() ,
,
解得MH=![]() ,
,
∴MN=2![]() ,
,
在Rt△MON中,ON=![]() =
=![]() =3
=3
Ⅱ.M'在∠AOB外部,如图2,过N点作QN⊥OM′,
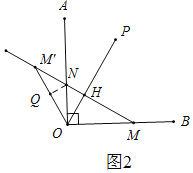
∵△ONM'为等腰三角形,即M′N=ON,
∴M′Q=![]() M′O,
M′O,
∵OM=![]() ,点M′与点M关于射线OP对称,
,点M′与点M关于射线OP对称,
∴M′Q=![]() ,OM=OM′,
,OM=OM′,
∴∠OM′M=∠OMM′,cos∠OM′M=![]() ,cos∠OMM′=
,cos∠OMM′=![]() ,
,
设ON=M′N=x,NH=M′H=y,
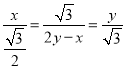 ,
,
解得:x=1,y=![]() ,
,
综上所述:当△ONM'为等腰三角形时,ON的长为3或1.
故答案为3,1.


科目:初中数学 来源: 题型:
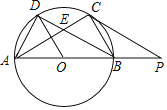
【题目】如图,AB是⊙O的直径,弦AC与BD交于点E,且AC=BD,连接AD,BC.
(1)求证:△ADB≌△BCA;
(2)若OD⊥AC,AB=4,求弦AC的长;
(3)在(2)的条件下,延长AB至点P,使BP=2,连接PC.求证:PC是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考体育测评前,某校在初三15个班中随机抽取了4个班的学生进行了摸底测评,将各班的满分人数进行整理,绘制成如下两幅统计图.
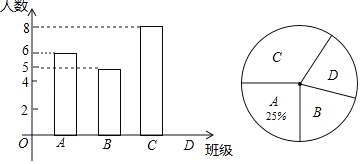
(1)D班满分人数共 人,扇形统计图中,表示C班满分人数的扇形圆心角的度数为 .
(2)这些满分同学中有4名同学(3女1男)的跳绳动作十分标准,学校准备从这4名同学中任选2名同学作示范,请利用画树状图或列表法求选中1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
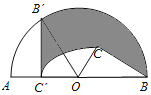
【题目】如图,C为半圆内一点,O为圆心,直径AB长为2cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为_____cm2.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M为等腰△ABD的底AB的中点,过D作DC∥AB,连结BC:AB=8cm.DM=4cm,DC=1cm,动点P自A点出发,在AB上匀速运动,动点Q自点B出发,在折线BC﹣CD上匀速运动,速度均为1cm/s,当其中一个动点到达终点时,它们同时停止运动,设点P运动(s)时,△MPQ的面积为S(不能构成△MPQ的动点除外).
(1)点Q在BC上运动时,求t的取值范围;
(2)当点Q在CD上运动时,求t为何值时,△MPQ是等腰三角形;
(3)求S与t之间的函数关系式;当t为何值时,S有最大值?最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.
(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,其中每辆大货车一次运费花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
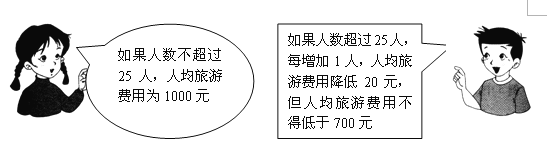 某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半⊙![]() 中,
中,![]() 是直径,点
是直径,点![]() 是⊙
是⊙![]() 上一点,点
上一点,点![]() 是
是![]() 的中点,
的中点,![]() 于点
于点![]() ,过点
,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,分别交
,分别交![]() 于点
于点![]() ,连接
,连接![]() ,关于下列结论:①
,关于下列结论:①![]() ;②
;②![]() ;③点
;③点![]() 是
是![]() 的外心;④
的外心;④![]() ,其中结论正确的是____.
,其中结论正确的是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() ,
,![]() 是常数,且
是常数,且![]() ),经过点
),经过点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(Ⅰ)求抛物线的解析式;
(Ⅱ)若点![]() 是射线
是射线![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,交抛物线于点
,交抛物线于点![]() ,设
,设![]() 点横坐标为
点横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,求出
,求出![]() 与
与![]() 之间的函数关系式,并写出相应的自变量
之间的函数关系式,并写出相应的自变量![]() 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,当点![]() 在线段
在线段![]() 上时,设
上时,设![]() ,已知
,已知![]() ,
,![]() 是以
是以![]() 为未知数的一元二次方程
为未知数的一元二次方程![]() (
(![]() 为常数)的两个实数根,点
为常数)的两个实数根,点![]() 在抛物线上,连接
在抛物线上,连接![]() ,
,![]() ,
,![]() ,且
,且![]() 平分
平分![]() ,求出
,求出![]() 值及点
值及点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com