练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在“双11”期间，新华商场销售某种冰箱，每台进价为3000元，调查发现，当销售价为3600元时，平均每天能售出16台，而当销售价每降低50元时，平均每天就能多售出4台. 假设每台冰箱降价元（x为50的整数倍，0<x<600）.

    （1）直接写出平均每天商场销售冰箱的数量y（台）与x（元）之间的关系；

    （2）要想这种冰箱的销售利润平均每天达到12800元，每台冰箱的定价应为多少元?

    【答案】（1）；（2）每台冰箱应定价为3400元.

    【解析】

    （1）根据题意找到y关于x的关系式即可；

    （2）根据利润=每台的利润×数量列出一个关于利润的方程，解方程即可.

    解：（1）

    即

    （2）根据题意,列方程：

    整理得

    解得

    ∴冰箱的定价为3600-200=3400.

    所以，要想这种冰箱的销售利润平均每天达到12800元，每台冰箱的定价应为3400元.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知AB是⊙O的直径，AT是⊙O的切线，∠ABT=50°，BT交⊙O于点C，E是AB上一点，延长CE交⊙O于点D.

    (1)如图①，求∠T和∠CDB的大小；

    (2)如图②，当BE=BC，求∠CDO的大小.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，D是AC上一点，BE∥AC，BE＝AD，AE分别交BD、BC于点F、G，∠1＝∠2．若DF＝8，FG＝4，则GE＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程

    (1)=4

    (2)3+2x-1=0

    (3)3x(x﹣2)=2(x﹣2)

    (4)+2x﹣3=0.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

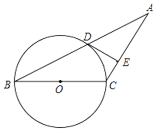
    【题目】如图，已知等腰三角形ABC的底角为30°，以BC为直径的⊙O与底边AB交于点D，过D作DE⊥AC，垂足为E．

    （1）证明：DE为⊙O的切线；

    （2）若BC＝4，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

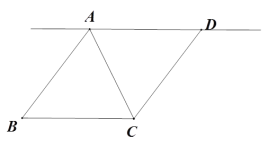
    【题目】如图，在菱形中，对角线、交于点，已知，．

    （1）求的长；

    （2）点为直线上的一个动点，连接，将线段绕点顺时针旋转的角度后得到对应的线段（即，交于点．

    ①当时，求的长；

    ②连接、，当的长度最小时，求的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的方程x2﹣2x+m﹣1＝0．

    （1）若方程有两个不相等的实数根，求m的取值范围；

    （2）若方程有一个实数根是5，求m的值及此时方程的另一个根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

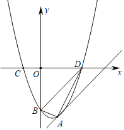
    【题目】如图，抛物线y＝x2﹣2x+c的顶点A在直线l：y＝x﹣a上，点D（3，0）为抛物线上一点．

    （1）求a的值；

    （2）抛物线与y轴交于点B，试判断△ABD的形状．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，点C为⊙O上一点，点P是半径OB上一动点（不与O，B重合），过点P作射线l⊥AB，分别交弦BC，于D、E两点，在射线l上取点F，使FC＝FD．

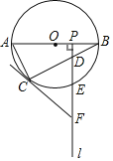
    （1）求证：FC是⊙O的切线；

    （2）当点E是的中点时，

    ① 若∠BAC＝60°，判断以O，B，E，C为顶点的四边形是什么特殊四边形，并说明理由；

    ② 若，且AB＝20，求OP的长．

    查看答案和解析>>

    同步练习册答案