
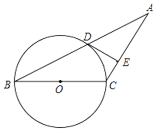
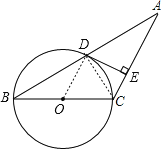
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)若BC=4,求DE的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接OD,由平行线的判定定理可得OD∥AC,利用平行线的性质得∠ODE=∠DEA=90°,可得DE为⊙O的切线;
(2)连接CD,由BC为直径,利用圆周角定理可得∠ADC=90°,由∠A=30°,AC=BC=4,利用锐角三角函数可得DE.
(1)证明:连接OD,
∵OD=OB,
∴∠ODB=∠B,
∵AC=BC,
∴∠A=∠B,
∴∠ODB=∠A,
∴OD∥AC,
∴∠ODE=∠DEA=90°,
∴DE为⊙O的切线;
(2)解:连接CD,
∵BC为直径,
∴∠ADC=90°,
∵∠A=30°,
又∵AC=BC=4,
∴AD=ACcos30°=4×![]() =2
=2![]() ,
,
∴DE=![]() AD=
AD=![]() .
.


科目:初中数学 来源: 题型:
【题目】为了了解班级学生数学课前预习的具体情况,郑老师对本班部分学生进行了为期一个月的跟踪调查,他将调查结果分为四类:A:很好;B:较好;C:一般;D:不达标,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)C类女生有 名,D类男生有 名,将上面条形统计图补充完整;
(2)扇形统计图中“课前预习不达标”对应的圆心角度数是 ;
(3)为了共同进步,郑老师想从被调查的A类和D类学生中各随机机抽取一位同学进行“一帮一”互助学习,请用画树状图或列表的方法求出所选两位同学恰好是一男一女同学的概率,
查看答案和解析>>
科目:初中数学 来源: 题型:
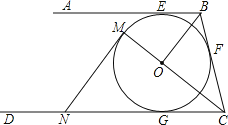
【题目】如图,AB、BC、CD分别与⊙O切于E、F、G,且AB∥CD.连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.
(1)求证:MN是⊙O的切线;
(2)当OB=6cm,OC=8cm时,求⊙O的半径及MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,

(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“双11”期间,新华商场销售某种冰箱,每台进价为3000元,调查发现,当销售价为3600元时,平均每天能售出16台,而当销售价每降低50元时,平均每天就能多售出4台. 假设每台冰箱降价![]() 元(x为50的整数倍,0<x<600).
元(x为50的整数倍,0<x<600).
(1)直接写出平均每天商场销售冰箱的数量y(台)与x(元)之间的关系;
(2)要想这种冰箱的销售利润平均每天达到12800元,每台冰箱的定价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导节能环保,降低能源消耗,提倡环保型新能源开发,造福社会.某公司研发生产一种新型智能环保节能灯,成本为每件40元.市场调查发现,该智能环保节能灯每件售价y(元)与每天的销售量为x(件)的关系如图,为推广新产品,公司要求每天的销售量不少于1000件,每件利润不低于5元.
(1)求每件销售单价y(元)与每天的销售量为x(件)的函数关系式并直接写出自变量x的取值范围;
(2)设该公司日销售利润为P元,求每天的最大销售利润是多少元?
(3)在试销售过程中,受国家政策扶持,毎销售一件该智能环保节能灯国家给予公司补贴m(m≤40)元.在获得国家每件m元补贴后,公司的日销售利润随日销售量的增大而增大,则m的取值范围是 (直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.

(1)求证:EF=MF;
(2)若AE=2,求FC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com