
【题目】如图,AB、BC、CD分别与⊙O切于E、F、G,且AB∥CD.连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.
(1)求证:MN是⊙O的切线;
(2)当OB=6cm,OC=8cm时,求⊙O的半径及MN的长.
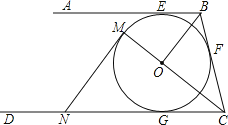
【答案】(1)见解析;(2)4.8cm,MN=9.6cm.
【解析】
(1)先由切线长定理和平行线的性质可求出∠OBC+∠OCB=90°,进而可求∠BOC=90°,然后证明∠NMC=90°,即可证明MN是⊙O的切线;
(2)连接OF,则OF⊥BC,根据勾股定理就可以求出BC的长,然后根据△BOC的面积就可以求出⊙O的半径,通过证明△NMC∽△BOC,即可求出MN的长.
(1)证明:∵AB、BC、CD分别与⊙O切于点E、F、G,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠DCB,
∠DCB,
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠OBC+∠OCB=![]() (∠ABC+∠DCB)=
(∠ABC+∠DCB)=![]() ×180°=90°,
×180°=90°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣90°=90°.
∵MN∥OB,
∴∠NMC=∠BOC=90°,
即MN⊥MC 且MO是⊙O的半径,
∴MN是⊙O的切线;
(2)解:连接OF,则OF⊥BC,
由(1)知,△BOC是直角三角形,
∴BC=![]() =
=![]() =10,
=10,
∵S△BOC=![]() OBOC=
OBOC=![]() BCOF,
BCOF,
∴6×8=10×OF,
∴OF=4.8cm,
∴⊙O的半径为4.8cm,
由(1)知,∠NCM=∠BCO,∠NMC=∠BOC=90°,
∴△NMC∽△BOC,
∴![]() ,即
,即![]() =
=![]() ,
,
∴MN=9.6(cm).



 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
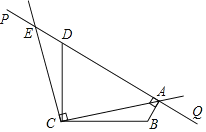
【题目】如图,∠BCD=90°,且BC=DC,直线PQ经过点D.设∠PDC=α(45°<α<135°),BA⊥PQ于点A,将射线CA绕点C按逆时针方向旋转90°,与直线PQ交于点E.
(1)当α=125°时,∠ABC= °;
(2)求证:AC=CE;
(3)若△ABC的外心在其内部,直接写出α的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,DE平分∠ADB,交AB于E,BF平分∠CBD,交CD于F.
(1)求证:△ADE≌△CBF;
(2)当AD与BD满足什么关系时,四边形DEBF是矩形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
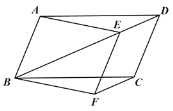
【题目】如图,在□ABCD中,点E是对角线BD上的一点,过点C作CF∥BD,且CF=DE,连接AE、BF、EF.
(1)求证:△ADE≌△BCF;
(2)若∠BFC-∠ABE=90°,判断四边形ABFE的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从点A开始沿边AB向B以1cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.
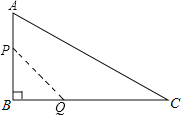
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
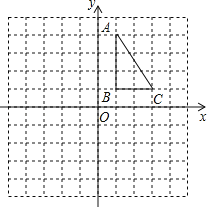
【题目】如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,4),B(1,1),C(3,1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加快“智慧校园”建设,某市准备为试点学校采购一批![]() 、
、![]() 两种型号的一体机,经过市场调查发现,今年每套
两种型号的一体机,经过市场调查发现,今年每套![]() 型一体机的价格比每套
型一体机的价格比每套![]() 型一体机的价格多0.6万元,且用960万元恰好能购买500套
型一体机的价格多0.6万元,且用960万元恰好能购买500套![]() 型一体机和200套
型一体机和200套![]() 型一体机.
型一体机.
(1)求今年每套![]() 型、
型、![]() 型一体机的价格各是多少万元
型一体机的价格各是多少万元
(2)该市明年计划采购![]() 型、
型、![]() 型一体机1100套,考虑物价因素,预计明年每套
型一体机1100套,考虑物价因素,预计明年每套![]() 型一体机的价格比今年上涨25%,每套
型一体机的价格比今年上涨25%,每套![]() 型一体机的价格不变,若购买
型一体机的价格不变,若购买![]() 型一体机的总费用不低于购买
型一体机的总费用不低于购买![]() 型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生每周平均课外阅读时间(单位: ![]() ), 随机抽查了该学校九年级部分同学,对其每周平均课外阅读时间进行统计,绘制了如下的统计图①和②,请根据相关信息,解答下列问题;
), 随机抽查了该学校九年级部分同学,对其每周平均课外阅读时间进行统计,绘制了如下的统计图①和②,请根据相关信息,解答下列问题;
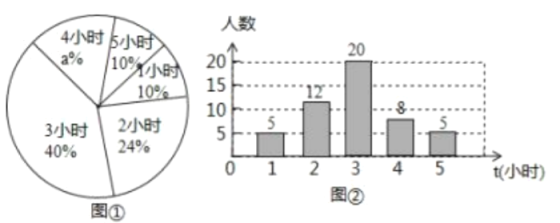
![]() 该校抽查九年级学生的人数为_______,图①中的 a值为______;
该校抽查九年级学生的人数为_______,图①中的 a值为______;
![]() 求统计的这组每周平均课外阅读时间的样本数据的平均数、众数和中位数;
求统计的这组每周平均课外阅读时间的样本数据的平均数、众数和中位数;
![]() 若该校九年级共有
若该校九年级共有![]() 名学生,根据统计的这组每周平均课外阅读时间的样本数据,估计该校九年级每周平均课外阅读时间为
名学生,根据统计的这组每周平均课外阅读时间的样本数据,估计该校九年级每周平均课外阅读时间为![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
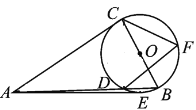
【题目】如图,Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E、F是⊙O上的两点,连结AE、CF、DF,满足EA=CA.
(1)求证:AE是⊙O的切线;
(2)若⊙O的半径是3,tan∠CFD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com