练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知关于x的方程x2﹣2x+m﹣1＝0．

    （1）若方程有两个不相等的实数根，求m的取值范围；

    （2）若方程有一个实数根是5，求m的值及此时方程的另一个根．

    【答案】（1）m＜2；（2）m＝﹣14，另一个根为﹣3．

    【解析】

    （1）根据方程的系数结合根的判别式△＞0，即可得出关于m的一元一次不等式，解之即可得出m的取值范围；
    （2）代入x=5可求出m的值，再利用两根之和等于-，即可求出方程的另一个根．

    （1）∵关于x的方程x2﹣2x+m﹣1＝0有两个不相等的实数根，

    ∴△＝（﹣2）2﹣4×1×（m﹣1）＞0，

    解得：m＜2，

    ∴m的取值范围为m＜2．

    （2）当x＝5时，原方程为52﹣2×5+m﹣1＝0，

    解得：m＝﹣14．

    ∵方程x2﹣2x+m﹣1＝0的一个实数根为5，

    ∴另一个根为2﹣5＝﹣3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】豆豆同学上周末对万州西山钟楼（AB）的高度进行了测量．如图，他站在点 D 处测得西山钟楼顶部点 A 的仰角为 67°．然后他从点 D 沿着坡度为 i=1:的斜坡 DF 方向走 20 米到达点 F，此时测得建筑物顶部点 A 的仰角为 45°．已知该同学的视线距地面高度为 1.6 米（即 CD＝EF＝1.6 米），图 中所有的点均在同一平面内，点 B、D、G 在同一条直线上，点 E、F、G 在同一条直线上，AB、CD、EF 均垂直于 BG.则西山钟楼 AB 的高约为（ ）（参考数据：sin67°≈0.92，cos67°≈0.39，tan67°≈2.36）

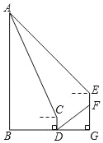
    A.17.4 米B.36.8 米C.48.8 米D.50.2 米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

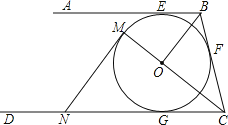
    【题目】如图，AB、BC、CD分别与⊙O切于E、F、G，且AB∥CD．连接OB、OC，延长CO交⊙O于点M，过点M作MN∥OB交CD于N．

    （1）求证：MN是⊙O的切线；

    （2）当OB＝6cm，OC＝8cm时，求⊙O的半径及MN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在“双11”期间，新华商场销售某种冰箱，每台进价为3000元，调查发现，当销售价为3600元时，平均每天能售出16台，而当销售价每降低50元时，平均每天就能多售出4台. 假设每台冰箱降价元（x为50的整数倍，0<x<600）.

    （1）直接写出平均每天商场销售冰箱的数量y（台）与x（元）之间的关系；

    （2）要想这种冰箱的销售利润平均每天达到12800元，每台冰箱的定价应为多少元?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，O是矩形ABCD的对角线的交点，作，，DE、CE相交于点E．求证：

    （1）四边形OCED是菱形；

    （2）连接OE．若，，求OE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y＝ax2+bx﹣4a（a≠0）经过A（﹣1，0）、C（0，4）两点，与x轴交于另一点B，连接AC，BC．

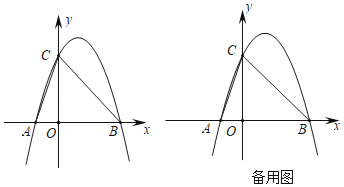
    （1）求抛物线的解析式；

    （2）过点C作x轴的平行线交抛物线于另一点D，连接BD，点P为抛物线上一点，且∠DBP＝45°，求点P的坐标；

    （3）在抛物线的对称轴上是否存在点M，使得由点M，A，C构成的△MAC是直角三角形？若存在，求出点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为倡导节能环保，降低能源消耗，提倡环保型新能源开发，造福社会．某公司研发生产一种新型智能环保节能灯，成本为每件40元．市场调查发现，该智能环保节能灯每件售价y（元）与每天的销售量为x（件）的关系如图，为推广新产品，公司要求每天的销售量不少于1000件，每件利润不低于5元．

    （1）求每件销售单价y（元）与每天的销售量为x（件）的函数关系式并直接写出自变量x的取值范围；

    （2）设该公司日销售利润为P元，求每天的最大销售利润是多少元？

    （3）在试销售过程中，受国家政策扶持，毎销售一件该智能环保节能灯国家给予公司补贴m（m≤40）元．在获得国家每件m元补贴后，公司的日销售利润随日销售量的增大而增大，则m的取值范围是　 　（直接写出结果）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

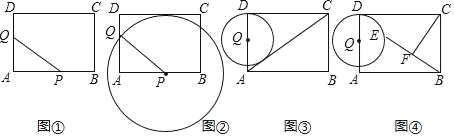
    【题目】在矩形ABCD中，AB＝8cm，BC＝6cm，点P从点A出发，沿AB边向点B以每秒2cm的速度移动，同时点Q从点D出发沿DA边向点A以每秒1cm的速度移动，P、Q其中一点到达终点时，另一点随之停止运动．设运动时间为t秒．回答下列问题：

    (1)如图①，几秒后△APQ的面积等于5cm2．

    (2)如图②，若以点P为圆心，PQ为半径作⊙P．在运动过程中，是否存在t值，使得点C落在⊙P上？若存在，求出t的值；若不存在，请说明理由．

    (3)如图③，若以Q为圆心，DQ为半径作⊙Q，当⊙Q与AC相切时

    ①求t的值．

    ②如图④，若点E是此时⊙Q上一动点，F是BE的中点，请直接写出CF的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

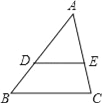
    【题目】如图，在△ABC中，D、E分别是AB、AC上的点，且DE∥BC，如果AD=2cm，DB=1cm，AE=1.8cm，则EC=（　　）

    A. 0.9cm B. 1cm C. 3.6cm D. 0.2cm

    【答案】A

    【解析】试题分析：根据平行线分线段成比例定理得到=，然后利用比例性质求EC的长．

    解：∵DE∥BC，

    ∴=，即=，

    ∴EC=0.9（cm）．

    故选A．

    考点：平行线分线段成比例．

    【题型】单选题
    【结束】
    6

    【题目】点C是线段AB的黄金分割点（AC>BC）,若AB=10cm，则AC等于（ ）

    A. 6 cm B. cm C. cm D. cm

    查看答案和解析>>

    同步练习册答案