
����Ŀ����ͼ��������y��ax2+bx��4a��a��0������A����1��0����C��0��4�����㣬��x�ύ����һ��B������AC��BC��
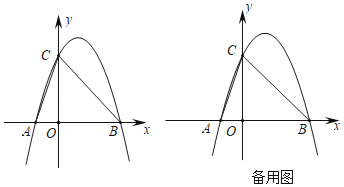
��1���������ߵĽ���ʽ��
��2������C��x���ƽ���߽�����������һ��D������BD����PΪ��������һ�㣬�ҡ�DBP��45�������P�����ꣻ
��3���������ߵĶԳ������Ƿ���ڵ�M��ʹ���ɵ�M��A��C���ɵ���MAC��ֱ�������Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y����x2+3x+4����2��P����![]() ��
��![]() ������3����M��������
������3����M��������![]() ��
��![]() ����
����![]() ����
����![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����
����
��������
��1��-4a=4����ã�a=-1���������ߵı���ʽΪ��y=-x2+bx+4������A�����������ʽ����ã�b=3��������⣻
��2���裺HR=BR=x����ER=4x��BD=5x=![]() ��
��![]() ��x��
��x��![]() ��BH��
��BH��![]() x��BG��1����GH��
x��BG��1����GH��![]() ��
��![]() ���ʵ�H��3��
���ʵ�H��3��![]() ��������B��4��0����ֱ��HB�ı���ʽΪ��y=
��������B��4��0����ֱ��HB�ı���ʽΪ��y= ![]() ���ڣ�
���ڣ�
�����٢ڲ���ã�x=4��-![]() ����ȥ4����������⣻
����ȥ4����������⣻
��3����AM��б�ߡ�CM��б�ߡ�AC��б������������ֱ���⼴�ɣ�
��1����4a��4����ã�a����1��
�������ߵı���ʽΪ��y����x2+bx+4��
����A�����������ʽ����ã�b��3��
�������ߵı���ʽΪ��y����x2+3x+4���٣�
��2�������ߵĶԳ���Ϊ��x��![]() ����D��3��4����
����D��3��4����
����D��x��Ĵ��߽�BP�ڵ�H����x���ڵ�G��
����H��HR��BD���R��
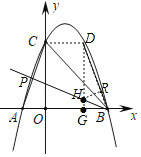
��BG��1��GD��4��tan��BDG��![]() ����DBP��45����
����DBP��45����
�裺HR��BR��x����DR��4x�� BD��5x��![]() ��
��![]() ��x��
��x��![]() �� BH��
�� BH��![]() x��BG��1����GH��
x��BG��1����GH��![]() ��
��![]() ���ʵ�H��3��
���ʵ�H��3��![]() ��������B��4��0����ͬ���ɵ�ֱ��HB�ı���ʽΪ��y����
��������B��4��0����ͬ���ɵ�ֱ��HB�ı���ʽΪ��y����![]() x+
x+![]() ���ڣ�
���ڣ�
�����٢ڲ���ã�x��4��![]() ����ȥ4����
����ȥ4����
�ʵ�P����![]() ��
��![]() ����
����
��3�����M��![]() ��m��������A����1��0������C��0��4������AM2��
��m��������A����1��0������C��0��4������AM2��![]() +m2��CM2��
+m2��CM2��![]() +��m��4��2��AC2��17��
+��m��4��2��AC2��17��
�ٵ�AM��б��ʱ��![]() +m2��
+m2��![]() +��m��4��2+17����ã�m��
+��m��4��2+17����ã�m��![]() ��
��
�ڵ�CM��б��ʱ��ͬ���ɵã�m����![]() ��
��
�۵�AC��б��ʱ��ͬ���ɵã�m��![]() ��
��![]() ��
��
���ϣ���M������Ϊ����![]() ��
��![]() ����
����![]() ����
����![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����
����


 ����ʦ���һ��һ��ϵ�д�
����ʦ���һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��AC��DΪBC����һ�㣬��AD��BD����ABC��36����

��1�����ADC�Ķ�����
��2����֤��DC��AB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У��Խ���
�У��Խ���![]() ��
��![]() ���ڵ�
���ڵ�![]() ����֪
����֪![]() ��
��![]() ��
��
��1����![]() �ij���
�ij���
��2����![]() Ϊֱ��
Ϊֱ��![]() �ϵ�һ�����㣬����
�ϵ�һ�����㣬����![]() �����߶�
�����߶�![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() �ĽǶȺ�õ���Ӧ���߶�
�ĽǶȺ�õ���Ӧ���߶�![]() ����
����![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
�ٵ�![]() ʱ����
ʱ����![]() �ij���
�ij���
������![]() ��
��![]() ����
����![]() �ij�����Сʱ����
�ij�����Сʱ����![]() �������
�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2��2x+m��1��0��
��1������������������ȵ�ʵ��������m��ȡֵ��Χ��
��2����������һ��ʵ������5����m��ֵ����ʱ���̵���һ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
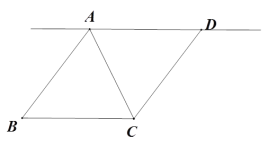
����Ŀ����ͼ���ֱ��ԡ�ABC�ı�AB��AC���������ȱ������Ρ�ABD�͡�ACE������BE��CD��
��1����֤��BE��CD��
��2����ADC���Կ����� ���Ƶ�A�� ��������˳ʱ����������ʱ��������ת���� ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
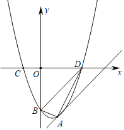
����Ŀ����ͼ��������y��x2��2x+c�Ķ���A��ֱ��l��y��x��a�ϣ���D��3��0��Ϊ��������һ�㣮
��1����a��ֵ��
��2����������y�ύ�ڵ�B�����жϡ�ABD����״��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2��4x+c��ͼ������ԭ�㣬��x�ύ�ڵ�A����4��0����

��1������κ����Ľ���ʽ��
��2�����������ϴ��ڵ�P������S��AOP=8����ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ������
������![]() �ı߳��ֱ�Ϊ4��6��
�ı߳��ֱ�Ϊ4��6��![]() ������Ӱ���ֵ������( )
������Ӱ���ֵ������( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com