
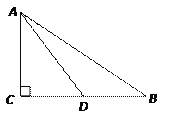
【题目】如图,在![]() 中,
中,![]() ,点D是BC边上的一点,
,点D是BC边上的一点,![]() ,
,![]() ,
,![]() .
.
(1)求AC和AB的长;
(2)求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题(1)在Rt△ACD中,利用![]() ,CD=6求出AD的长,再求出AC的长.再在Rt△ABC中,利用
,CD=6求出AD的长,再求出AC的长.再在Rt△ABC中,利用![]() =
=![]() =
=![]() 求出BC的长,再求出AB的长;(2)过点D作DH⊥AB于点H,利用S△ABD=
求出BC的长,再求出AB的长;(2)过点D作DH⊥AB于点H,利用S△ABD=![]() AB·DH=
AB·DH=![]() BD·AC,其中AB、BD、AC都可知,则可求出DH,再在Rt△ADH中利用正弦三角形函数定义求解.
BD·AC,其中AB、BD、AC都可知,则可求出DH,再在Rt△ADH中利用正弦三角形函数定义求解.
解:(1)∵在Rt△ACD中,cos∠ADC=![]() =
=![]() ,CD=6,
,CD=6,
∴AD=10,
∴在Rt△ACD中,AC=![]() =8.
=8.
又∵在Rt△ABC中,![]() =
=![]() =
=![]() ,
,
∴BC=12,
∴AB=![]() =4
=4![]() .
.
(2)过点D作DH⊥AB于点H,
∴S△ABD=![]() AB·DH=
AB·DH=![]() BD·AC,
BD·AC,
其中AB=4![]() ,BD=BC-CD=6,AC=8,
,BD=BC-CD=6,AC=8,
∴DH=![]() =
=![]() ,
,
∴在Rt△ADH中,sin∠BAD=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,如果AD=2cm,DB=1cm,AE=1.8cm,则EC=( )
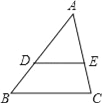
A. 0.9cm B. 1cm C. 3.6cm D. 0.2cm
【答案】A
【解析】试题分析:根据平行线分线段成比例定理得到![]() =
=![]() ,然后利用比例性质求EC的长.
,然后利用比例性质求EC的长.
解:∵DE∥BC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴EC=0.9(cm).
故选A.
考点:平行线分线段成比例.
【题型】单选题
【结束】
6
【题目】点C是线段AB的黄金分割点(AC>BC),若AB=10cm,则AC等于( )
A. 6 cm B. ![]() cm C.
cm C. ![]() cm D.
cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
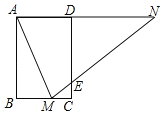
【题目】如图,矩形ABCD中,AB=3,BC=2,点M在BC上,连接AM,作∠AMN=∠AMB,点N在直线AD上,MN交CD于点E.
(1)求证:△AMN是等腰三角形;
(2)求证:AM2=2BMAN;
(3)当M为BC中点时,求ME的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
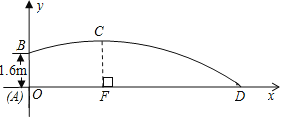
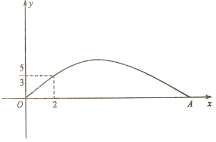
【题目】“阳光体育活动”促进了学校体育活动的开展,小杰在一次铅球比赛中,铅球出手以后的轨迹是抛物线的一部分(如图所示),已知铅球出手时离地面1.6米,铅球离投掷点3米时达到最高点,在离投掷点8米处落地,
(1)请求出此轨迹所在抛物线的关系式.
(2)设抛物线与X轴另一个交点是E,点Q是对称轴上的一个动点,求当△EBQ的周长最短时点Q的坐标.
(3)在抛物线上是否存在点G使得S△DEG=19.5,若存在请求出点G的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某场足球比赛中,球员甲在球门正前方点O处起脚射门,在不受阻挡的情况下,足球沿如图所示的抛物线飞向球门中心线,当足球飞行的水平距离为2 m时,高度为![]() ,落地点A距O点12 m.已知点O距球门9 m,球门的横梁高为2.44 m.
,落地点A距O点12 m.已知点O距球门9 m,球门的横梁高为2.44 m.
(1)飞行的足球能否射入球门?通过计算说明理由;
(2)若守门员乙站在球门正前方2 m处,他跳起时能摸到的最大高度为2.52 m,他能阻止此次射门吗?并写明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初2019级即将迎来中考,很多家长都在为孩子准备营养午餐.一家快餐店看准了商机,在5月5号推出了A,B,C三种营养套餐.套餐C单价比套餐A贵5元,三种套餐的单价均为整数,其中A套餐比C套餐少卖12份,B套餐比C套餐少卖6份,且C套餐当天卖出的数量大于26且不超过32,当天总销售量为偶数且当天销售额达到了1830元,商家发现C套餐很受欢迎,因此在6号加推出了C套餐升级版D套餐,四种套餐同时售卖,A套餐比5号销售量减少,C套餐比5号销售量增加![]() ,且A减少的份数比C套餐增加的份数多5份,B套餐销售量不变,由于商家人手限制,两天的总销售量相同,则其他套餐单价不变的情况下,D套餐至少比C套餐费贵______时,才能使6号销售额达到1950元.
,且A减少的份数比C套餐增加的份数多5份,B套餐销售量不变,由于商家人手限制,两天的总销售量相同,则其他套餐单价不变的情况下,D套餐至少比C套餐费贵______时,才能使6号销售额达到1950元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=-![]() x2+
x2+![]() x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C:连接BC,点P为线段BC上方抛物线上的一动点,连接OP交BC于点Q.
x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C:连接BC,点P为线段BC上方抛物线上的一动点,连接OP交BC于点Q.
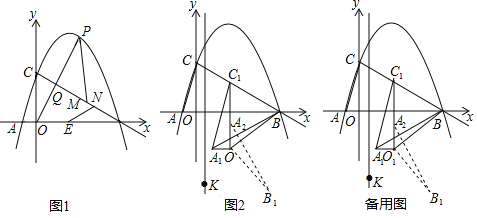
(1)如图1,当![]() 值最大时,点E为线段AB上一点,在线段BC上有两动点M,N(M在N上方),且MN=1,求PM+MN+NE-
值最大时,点E为线段AB上一点,在线段BC上有两动点M,N(M在N上方),且MN=1,求PM+MN+NE-![]() BE的最小值;
BE的最小值;
(2)如图2,连接AC,将△AOC沿射线CB方向平移,点A,C,O平移后的对应点分别记作A1,C1,O1,当C1B=O1B时,连接A1B、O1B,将△A1O1B绕点O1沿顺时针方向旋转90°后得△A2O1B1在直线x=![]() 上是否存在点K,使得△A2B1K为等腰三角形?若存在,直接写出点K的坐标;不存在,请说明理由.
上是否存在点K,使得△A2B1K为等腰三角形?若存在,直接写出点K的坐标;不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA、OC分别在x轴、y轴上,B点坐标是(8,4),将△AOC沿对角线AC翻折得△ADC,AD与BC相交于点E.
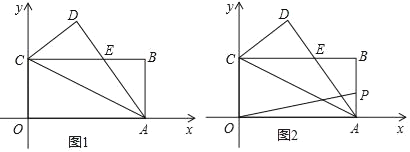
(1)求证:△CDE≌△ABE
(2)求E点坐标;
(3)如图2,动点P从点A出发,沿着折线A→B→C→O运动(到点O停止),是否存在点P,使得△POA的面积等于△ACE的面积,若存在,直接写出点P坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com