
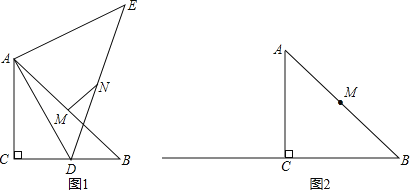
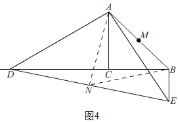
【题目】如图,等腰直角三角形ABC中,∠ACB=90°.D为射线BC上一动点.连接AD,将线段AD绕点A逆时针旋转90°至点E,连接AE、DE.点M、N分别是AB、DE的中点,连接MN.
(1)如图1,点D在线段BC上.
①猜想MN与AB的位置关系,并证明你的猜想;
②连接EB,猜想BE与BC的位置关系;
(2)在图2中,若点D在线段BC的延长线上,BE与BC的位置关系是否改变?请你补全图形后,证明你的猜想.
【答案】(1)①垂直,证明见解析;②垂直,理由见解析;(2)垂直,理由见解析.
【解析】
(1)①先判断出AD=![]() AN,AC=
AN,AC=![]() AM,进而得出
AM,进而得出![]() ,判断出△CAD∽△MAN,即可得出结论;
,判断出△CAD∽△MAN,即可得出结论;
②先判断出MN是AB的中垂线,得出AN=BN,再判断出AN=DN=EN=![]() DE,进而得出DN=EN=BN,最后用三角形的内角和即可得出结论;
DE,进而得出DN=EN=BN,最后用三角形的内角和即可得出结论;
(2)分两种情况,同(1)②的方法,即可得出结论.
(1)①垂直,
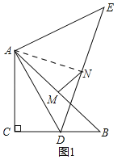
理由:如图1,
由旋转知,AD=AE,∠DAE=90°,
∵点N是DE的中点,
∴∠DAN=∠![]() ∠DAE=45°,∠AND=90°,
∠DAE=45°,∠AND=90°,
∴AD=![]() AN,
AN,
∴![]() =
=![]() ,
,
在等腰直角三角形ABC中,∠ACB=90°,
∴∠BAC=45°,AB=![]() AC,
AC,
∵M是AB的中点,
∴AM=![]() AB=
AB=![]() AC,
AC,
∴AC=![]() AM,
AM,
∴![]() ,
,
∴![]() ,
,
∵∠DAN=∠BAC=45°,
∴∠CAD=∠MAN,
∴△CAD∽△MAN,
∴∠AMN=∠ACD=90°,
∴MN⊥AB;
②垂直;
理由:如图2,
连接AB,BN,由①知,MN⊥AB,
∵M是AB的中点,
∴MN是AB的中垂线,
∴AN=BN,
由旋转知,AD=AE,∠DAE=90°,
∴点N是DE的中点,
∴AN=DN=EN=![]() DE,
DE,
∴DN=EN=BN,
∴∠BDN=∠DBN,∠BEN=∠EBN,
∵∠BDE+∠BED+∠DBE=180°,
∴∠BDN+∠BEN+∠DBN+∠EBN=2∠DBN+2∠EBN=2(∠DBN+∠EBN)=2∠DBE=180°,
∴∠DBE=90°,
∴BE⊥BC;
(2)关系不改变,DE⊥BC,
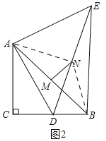
理由:当CD<AC时,如图3,
同(1)②的方法;
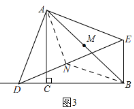
当CD>AC时,如图4,
同(1)②的方法.


科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成相应的任务:
我们知道,利用尺规作已知线段的垂直平分线可以得到该线段的中点、四等分点、……怎样得到线段的三等分点呢?如图,已知线段MN,用尺规在MN上求作点P,使![]() .
.
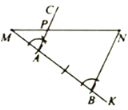
小颖的作法是:
①作射线MK(点K不在直线MN上);
②在射线MK上依次截取线段MA,AB,使![]() ,连接BN;
,连接BN;
③作射线![]() ,交MN于点P点P即为所求作的点.
,交MN于点P点P即为所求作的点.
小颖作法的理由如下:
∵![]() (作法),∴
(作法),∴![]()
∵![]() (已知),
(已知),![]() (等量代换)
(等量代换)
∵![]() (线段和差定义),∴
(线段和差定义),∴![]() (等量代换,等式性质)
(等量代换,等式性质)
数学思考:(1)小颖作法理由中所缺的依据是:________________________________.
拓展应用:(2)如图,已知线段a,b,c,求作线段d,使![]()
a. ![]() b.
b. ![]() c.
c. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,垂足为E,如果AB=5,AE=4,BC=8,有下列结论:
①DE=4![]() ;
;
②S△AED=![]() S四边形ABCD;
S四边形ABCD;
③DE平分∠ADC;
④∠AED=∠ADC.
其中正确结论的序号是_____(把所有正确结论的序号都填在横线上)

查看答案和解析>>
科目:初中数学 来源: 题型:
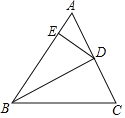
【题目】如图,在△ABC中,点BD⊥AC于点D,DE⊥AB于点E,BD2=BCBE.
(1)求证:△BCD∽△BDE;
(2)如果BC=10,AD=6,求AE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
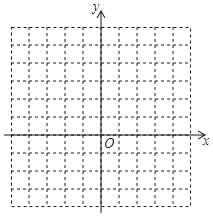
【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)与y轴的交点坐标是 ,顶点坐标是 .
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |
(3)结合图象回答:当﹣2<x<2时,函数值y的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
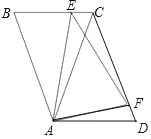
【题目】如图,在平行四边形ABCD中,AC=CD.点E、F分别为边BC、CD上的两点,且∠EAF=∠CAD
(1)求证:∠D=∠ACB:
(2)求证:△ADF∽△ACE:
(3)求证:AE=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在![]() 中,
中,![]() ,
,![]() ,D是BC的中点.
,D是BC的中点.
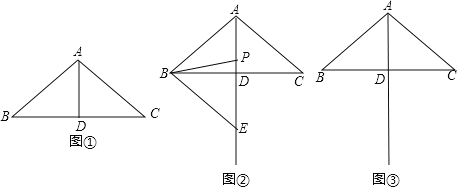
小明对图①进行了如下探究:在线段AD上任取一点P,连接PB.将线段PB绕点P按逆时针方向旋转![]() ,点B的对应点是点E,连接BE,得到
,点B的对应点是点E,连接BE,得到![]() .小明发现,随着点P在线段AD上位置的变化,点E的位置也在变化,点E可能在直线AD的左侧,也可能在直线AD上,还可能在直线AD的右侧.请你帮助小明继续探究,并解答下列问题:
.小明发现,随着点P在线段AD上位置的变化,点E的位置也在变化,点E可能在直线AD的左侧,也可能在直线AD上,还可能在直线AD的右侧.请你帮助小明继续探究,并解答下列问题:
(1)当点E在直线AD上时,如图②所示.
①![]() ;②连接CE,直线CE与直线AB的位置关系是 .
;②连接CE,直线CE与直线AB的位置关系是 .
(2)请在图③中画出![]() ,使点E在直线AD的右侧,连接CE.试判断直线CE与直线AB的位置关系,并说明理由.
,使点E在直线AD的右侧,连接CE.试判断直线CE与直线AB的位置关系,并说明理由.
(3)当点P在线段AD上运动时,求AE的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P的坐标为(![]() ,
,![]() ),点Q的坐标为(
),点Q的坐标为(![]() ,
,![]() ),且
),且![]() ,
,![]() ,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.下图为点P,Q 的“相关矩形”的示意图.
,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.下图为点P,Q 的“相关矩形”的示意图.
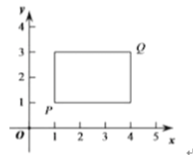
(1)已知点A的坐标为(1,0).
①若点B的坐标为(3,1)求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)⊙O的半径为![]() ,点M的坐标为(m,3).若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
,点M的坐标为(m,3).若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=k1x+b的图象与反比例函数y=![]() 的图象交于A(3,﹣2)、B(﹣2,n)两点,与x轴交于点C.
的图象交于A(3,﹣2)、B(﹣2,n)两点,与x轴交于点C.
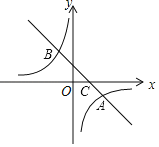
(1)求k2,n的值;
(2)请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)将x轴下方的图象沿x轴翻折,点A落在点A′处,连接A'B、A'C,求△A'BC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com