
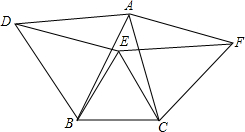
 如图,以△ABC的三边分别作等边△ABD,△BCE,△ACF.
如图,以△ABC的三边分别作等边△ABD,△BCE,△ACF.分析 (1)可先证明△ABC≌△DBE,可得DE=AC,又有AC=AF,可得DE=AF,同理可得AD=EF,根据两组对边分别相等的四边形是平行四边形,可证四边形ADEF是平行四边形;
(2)不一定,当∠BAC=60°时不存在.
解答 (1)证明:∵△ABD,△BCE都是等边三角形,
∴∠DBE=∠ABC=60°-∠ABE,
在△ABC和△DBE中,$\left\{\begin{array}{l}{DB=AB}\\{∠ABC=∠DBE}\\{BE=BC}\end{array}\right.$,
∴△ABC≌△DBE(SAS).
∴DE=AC.
又∵AC=AF,
∴DE=AF.
同理可得EF=AD.
∴四边形ADEF是平行四边形.
(2)解:不一定,当∠BAC=60°时,∠DAF=180°,不存在四边形ADEF.
点评 本题主要考查了等边三角形的性质,平行四边形的判定,关键是掌握等边三角形三边相等,三个角都是60°,两组对边分别相等的四边形是平行四边形.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:解答题
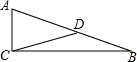 如图,一位同学做了一个斜面装置进行科学实验,△ABC是该装置左视图,∠ACB=90°,∠B=15°,为了加固斜面,在斜面AB的中点D处连结一条支撑杆CD,量得CD=6.
如图,一位同学做了一个斜面装置进行科学实验,△ABC是该装置左视图,∠ACB=90°,∠B=15°,为了加固斜面,在斜面AB的中点D处连结一条支撑杆CD,量得CD=6.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
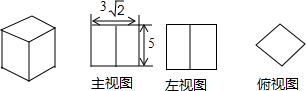 一个长方体的三视图如图所示,若其俯视图为正方形,则长方体的高和底面边长分别为( )
一个长方体的三视图如图所示,若其俯视图为正方形,则长方体的高和底面边长分别为( )| A. | 5,3$\sqrt{2}$ | B. | 2,3$\sqrt{2}$ | C. | 3,5 | D. | 5,3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
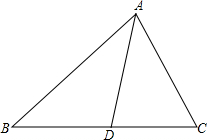 如图,小明和小刚住在同一小区(A点),每天一块去学校(B点)上学,一天,小明要先去文具店(C点)买练习本再去学校,小刚要先去书店(D点)买书再去学校,问:这天两人从家到学校谁走的路远?为什么?
如图,小明和小刚住在同一小区(A点),每天一块去学校(B点)上学,一天,小明要先去文具店(C点)买练习本再去学校,小刚要先去书店(D点)买书再去学校,问:这天两人从家到学校谁走的路远?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
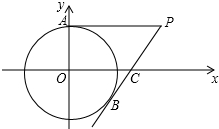 如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C
如图,在平面直角坐标系中,以点O为圆心,半径为2的圆与y轴交于点A,点P(4,2)是⊙O外一点,连接AP,直线PB与⊙O相切于点B,交x轴于点C查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y1>y2 | D. | y2>y1>y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
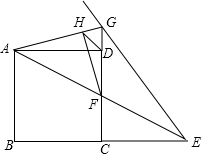 如图,点E是正方形ABCD的边BC延长线一点,连接AE交CD于F,作∠AEG=∠AEB,EG交CD的延长线于G,连接AG,当CE=BC=2时,作FH⊥AG于H,连接DH,则DH的长为( )
如图,点E是正方形ABCD的边BC延长线一点,连接AE交CD于F,作∠AEG=∠AEB,EG交CD的延长线于G,连接AG,当CE=BC=2时,作FH⊥AG于H,连接DH,则DH的长为( )| A. | 2-$\sqrt{2}$ | B. | $\sqrt{2}-1$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -52=(-5)×(-5) | B. | 32=3×2 | C. | 32=3+3 | D. | -(-$\frac{1}{2}$)2=-$\frac{1}{2}$×$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com