
分析 (1)由$\frac{1}{x×3x}$=$\frac{1}{2{x}^{2}}$(1-$\frac{1}{3}$),$\frac{1}{3x×5x}$=$\frac{1}{2{x}^{2}}$($\frac{1}{3}$-$\frac{1}{5}$),$\frac{1}{5x×7x}$=$\frac{1}{2{x}^{2}}$($\frac{1}{5}$-$\frac{1}{7}$)…-,进一步代入抵消计算得出答案即可;
(2)把x=2代入(1)中的化简结果,求得数值即可.
解答 解:(1)$\frac{1}{x×3x}$-+$\frac{1}{3x×5x}$+$\frac{1}{5x×7x}$+$\frac{1}{7x×9x}$+…+$\frac{1}{17x×19x}$
=$\frac{1}{2{x}^{2}}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+$\frac{1}{9}$+…+$\frac{1}{17}$-$\frac{1}{19}$)
=$\frac{1}{2{x}^{2}}$(1-$\frac{1}{19}$)
=$\frac{1}{2{x}^{2}}$×$\frac{18}{19}$
=$\frac{9}{19{x}^{2}}$;
(2)当x=2时,
原式=$\frac{9}{76}$.
点评 此题考查分式的化简求值,找出拆分的方法,得出运算规律,运用规律拆分计算即可.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
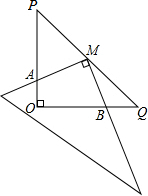 如图,在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.
如图,在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com