
分析 先找到整数的平方在600000和700000的取值范围,完全平方数,再找到其中整数的个位是4和6的平方数,即为所求完全平方数.
解答 解:∵一个六位数6xyzx6(x、y、z可以相同)是完全平方数,
774<$\sqrt{600000}$<$\sqrt{700000}$<837,
由于六位数的个位数字是6,
∴所有这样的六位数为7762=602176,7842=614656,7862=617796,7942=630436,7962=633616,8042=646416,8062=649636,8142=662596,8162=665856,8242=678976,8262=682276,8342=695556,8362=698896.
故答案为:602176,614656,617796,630436,633616,646416,649636,662596,665856,8242=678976,682276,695556,698896.
点评 本题考查了完全平方数的性质,整数的平方末位数字只能是0,1,4,5,6,9,凡是末位数字为2,3,7,8的整数必不是平方数,这是重点又是难点,要熟练掌握.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
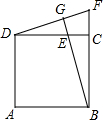 如图所示,在正方形ABCD中,E为CD上一点,延长BC至F,使CF=CE,连接DF,BE与DF相交于点G,则下面结论错误的是( )
如图所示,在正方形ABCD中,E为CD上一点,延长BC至F,使CF=CE,连接DF,BE与DF相交于点G,则下面结论错误的是( )| A. | BE=DF | B. | BG⊥DF | C. | ∠F+∠CEB=90° | D. | ∠FDC+∠ABG=90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com