
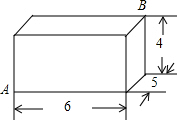
 如图,有一个长方体盒子,长、宽、高分别为6cm、5cm、4cm,有一只小虫要从点A处沿长方体表面爬到点B处,最短的路径长为$\sqrt{117}$cm.
如图,有一个长方体盒子,长、宽、高分别为6cm、5cm、4cm,有一只小虫要从点A处沿长方体表面爬到点B处,最短的路径长为$\sqrt{117}$cm. 分析 蚂蚁有三种爬法,就是把正视和俯视(或正视和侧视,或俯视和侧视)二个面展平成一个长方形,然后求其对角线,比较大小即可求得最短的途径.
解答 解:路径一:AB=$\sqrt{(5+6)^{2}+{4}^{2}}=\sqrt{137}$;
路径二:AB=$\sqrt{(5+4)^{2}+{6}^{2}}=\sqrt{117}$;
路径三:AB=$\sqrt{(4+6)^{2}+{5}^{2}}=\sqrt{125}$;
∵$\sqrt{137}$>$\sqrt{125}$>$\sqrt{117}$,
∴$\sqrt{117}$cm为最短路径.
故答案为:$\sqrt{117}$
点评 此题考查最短途径问题,关键是把长方体拉平后用了勾股定理求出对角线的长度.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
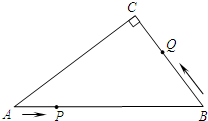 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=6,若点P是边AB上的一个动点,以每秒3个单位的速度按照从A→B→A运动,同时点Q从B→C以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动.在运动过程中,设运动时间为t,若△BPQ为直角三角形,则t的值为$\frac{12}{5}$、$\frac{24}{7}$、$\frac{24}{5}$.
如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=6,若点P是边AB上的一个动点,以每秒3个单位的速度按照从A→B→A运动,同时点Q从B→C以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动.在运动过程中,设运动时间为t,若△BPQ为直角三角形,则t的值为$\frac{12}{5}$、$\frac{24}{7}$、$\frac{24}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com