
【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=2,P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )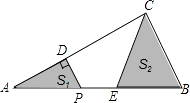
A.一直减小
B.一直不变
C.先增大后减小
D.先减小后增大
科目:初中数学 来源: 题型:
【题目】合并同类项:
(1)-a-a-a;
(2)3a2-5a2+9a2;
(3)2a2-3ab+4b2-5ab-6b2;
(4)xy-![]() x2y2-
x2y2-![]() xy-
xy-![]() x2y2.
x2y2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx-1与x轴、y轴分别交于B、C两点,OB:OC=![]() .
.
(1)求B点的坐标和k的值.
(2)若点A(x,y)是第一象限内的直线y=kx-1上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;
(3)在(2)的条件下,当点A运动到什么位置时,△AOB的面积是![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(4,5)、B(1,0)、C(4,0).
(1)画出△ABC关于y轴的对称图形△A1B1C1,并写出A1点的坐标;
(2)在y轴上求作一点P,使△PAB的周长最小,并求出点P的坐标及△PAB的周长最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
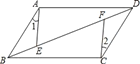
A. BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△ADE都是等腰直角三角形, ∠BAC=∠DAE=90°.
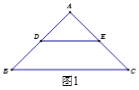
(1)如图1,点D、E在AB、AC上,则BD,CE满足怎样的数量关系和位置关系?(直接写出答案)
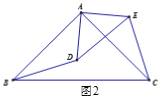
(2)如图2,点D在△ABC内部, 点E在△ABC外部,连结BD, CE, 则BD,CE满足怎样的数量关系和位置关系?请说明理由.
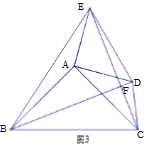
(3)如图3,点D,E都在△ABC外部,连结BD, CE, CD, EB,BD, 与CE相交于H点. 若BD=![]() ,求四边形BCDE的面积.
,求四边形BCDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠ACB=90°,BC=5,点 P 在边 AB 上,连接 CP.将△BCP 沿直线CP 翻折后,点 B 恰好落在边 AC 的中点处,则点 P 到 AC 的距离是( )

A. 2.5 B. ![]() C. 3.5 D.
C. 3.5 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com