练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】合并同类项：

    (1)－a－a－a；

    (2)3a2－5a2＋9a2；

    (3)2a2－3ab＋4b2－5ab－6b2；

    (4)xy－x2y2－xy－x2y2.

    【答案】(1)－3a;(2) 7a2;(3) 2a2－8ab－2b2;(4) xy－x2y2

    【解析】

    （1）根据合并同类项法则直接计算即可；（2）根据合并同类项法则直接计算即可；（3）先确定同类项，再根据合并同类项法则直接计算即可；（4）先确定同类项，再根据合并同类项法则直接计算即可.

    (1)－a－a－a=(-1-1-1)a=-3a；

    (2)3a2－5a2＋9a2=（3-5+9）a2=7a2；

    (3)2a2－3ab＋4b2－5ab－6b2=2a2－3ab－5ab＋4b2－6b2=2a2－8ab－2b2；

    (4)xy－x2y2－xy－x2y2 =xy－xy－x2y2－x2y2=xy－x2y2.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

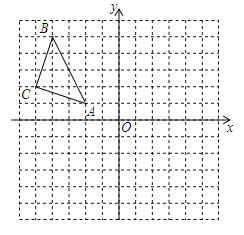
    【题目】如图，△ABC在平面直角坐标系中，点A、B、C的坐标分别为A（﹣2，1），B（﹣4，5），C（﹣5，2）．

    （1）作△ABC关于y对称的△A1B1C1，其中，点A、B、C的对应点分别为A1、B1、C1（不要求写作法）；

    （2）写出点A1、B1、C1的坐标；

    （3）计算△A1B1C1的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列各式，能够表示图中阴影部分的面积的是（　　）

    ①ac+（b﹣c）c；②ac+bc﹣c2；③ab﹣（a﹣c）（b﹣c）；④（a﹣c）c+（b﹣c）c+c2

    A. ①②③④ B. ①②③ C. ①② D. ①

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＞AC，AD平分∠BAC

    （1）尺规作图：在AD上标出一点P，使得点P到点B和点C的距离相等（不写作法，但必须保留作图痕迹）；

    （2）过点P作PE⊥AB于点E，PF⊥AC于点F，求证：BE=CF；

    （3）若AB=a，AC=b，则BE=　 　，AE=　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料

    小明遇到这样一个问题：求计算所得多项式的一次项系数．

    小明想通过计算所得的多项式解决上面的问题，但感觉有些繁琐，他想探寻一下，是否有相对简洁的方法．

    他决定从简单情况开始，先找所得多项式中的一次项系数．通过观察发现：

    也就是说，只需用中的一次项系数1乘以中的常数项3，再用中的常数项2乘以中的一次项系数2，两个积相加，即可得到一次项系数．

    延续上面的方法，求计算所得多项式的一次项系数．可以先用的一次项系数1， 的常数项3， 的常数项4，相乘得到12；再用的一次项系数2， 的常数项2， 的常数项4，相乘得到16；然后用的一次项系数3， 的常数项2， 的常数项3，相乘得到18．最后将12，16，18相加，得到的一次项系数为46．

    参考小明思考问题的方法，解决下列问题：

    （1）计算所得多项式的一次项系数为 ．

    （2）计算所得多项式的一次项系数为 ．

    （3）若计算所得多项式的一次项系数为0，则=_________．

    （4）若是的一个因式，则的值为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先化简，再求值：

    (1)－a2b＋(3ab2－a2b)－2(2ab2－a2b)，其中a＝1，b＝－2；

    (2)－6x＋3(3x2－1)－(9x2－x＋3)，其中x＝－.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将一张如图①所示的长方形铁皮四个角都剪去边长为30cm的正方形，再四周折起，做成一个有底无盖的铁盒，如图②.铁盒底面长方形的长是4acm，宽是3acm.

    (1)请用含有a的代数式表示图①中原长方形铁皮的面积；

    (2)若要在铁盒的外表面涂上某种油漆，每1元钱可涂油漆的面积为cm2，则在这个铁盒的外表面涂上油漆需要多少钱(用含有a的代数式表示)?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个木箱中装有卡片共50张，这些卡片共有三种，它们分别标有1、2、3的字样，除此之外其他都相同，其中标有数字2的卡片的张数是标有数字3卡片的张数的3倍少8张．已知从箱子中随机摸出一张标有数字1卡片的概率是 ．
    （1）求木箱中装有标1的卡片张数；
    （2）求从箱子中随机摸出一张标有数字3的卡片的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，AC=4，BC=2，P是AB边上一动点，PD⊥AC于点D，点E在P的右侧，且PE=1，连结CE．P从点A出发，沿AB方向运动，当E到达点B时，P停止运动．在整个运动过程中，图中阴影部分面积S1+S2的大小变化情况是（ ）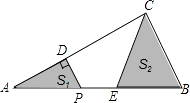

    A.一直减小
    B.一直不变
    C.先增大后减小
    D.先减小后增大

    查看答案和解析>>

    同步练习册答案