
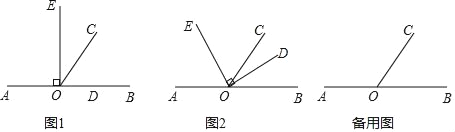
【题目】如图所示,在直线AB上的一点O,以O为端点依次作射线OE,OC,OD,使∠EOD=90°,∠COB=60°
(1)如图1当∠EOD的一边OD在射线OB上时,求∠COE的度数;
(2)如图2当∠EOD绕着点O逆时针旋转到OC平分∠BOE时,求∠COD的度数;
(3)当∠EOD绕着点O逆时针旋转,且O°<∠AOE<90°(但≠60°)时,试猜想∠AOE与∠COD有怎样的数量关系,并说明理由.
【答案】(1)30;(2)30°;(3)当60°<∠AOE<90°时,∠AOE﹣∠COD=30°;当0<∠AOE<60°时,∠AOE+∠COD=30°;
【解析】
(1)根据∠COE=∠EOB-∠BOC计算即可;
(2)根据∠COD=∠EOD-∠EOC,只要求出∠EOC即可;
(3)当60°<∠AOE<90°时,∠AOE-∠COD=30°;当0<∠AOE<60°时,∠AOE+∠COD=30°.
(1)∵∠COE=∠EOB﹣∠BOC,∠EOD=90°,∠COB=60°
∴∠COE=90°﹣60°=30°,
(2)∵OC 平分∠BOE,
∴∠BOC=∠COE=60°,
∴∠COD=∠EOD﹣∠EOC=90°﹣60°=30°;
(3)①如图2中,当60°<∠AOE<90°时,
∵∠EOD=90°,
∴∠AOE+∠DOB=90°,
∴∠AOE+(60°﹣∠COD)=90°,
∴∠AOE﹣∠COD=30°
②如图3中,当0<∠AOE<60°时,∵∠AOC=180°﹣∠BOC=120°,∠EOD=90°,
∴∠AOE+∠COD=30°;
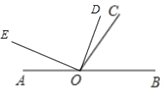
综上所述,当60°<∠AOE<90°时,∠AOE﹣∠COD=30°;
当0<∠AOE<60°时,∠AOE+∠COD=30°.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
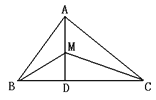
【题目】如图所示,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
A. 9 B. 35 C. 45 D. 无法计算
查看答案和解析>>
科目:初中数学 来源: 题型:
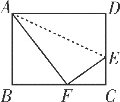
【题目】如图,已知长方形ABCD中AB = 8cm,BC = 10cm,在边CD上取一点E,将△ADE折叠,使点D恰好落在BC边上的点F,则CF的长为( )
A. 2cm B. 3cm C. 4cm D. 5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠BCD=∠A. 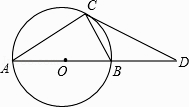
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为3,CD=4,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,等边△AOB的边长为6,点C在边OA上,点D在边AB上,且OC=3BD,反比例函数y= ![]() (k≠0)的图象恰好经过点C和点D,则k的值为( )
(k≠0)的图象恰好经过点C和点D,则k的值为( ) 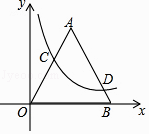
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E是平面内异于点A的任意一点,以线
段AE为边作正方形AEFG,连接EB,GD.
(1) 如图1,判断EB与GD的关系并说明理由;
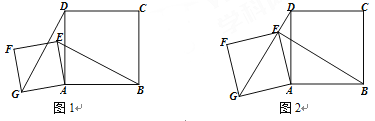
(2) 如图2,若点E在线段DG上,AB=5,AG=3![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图, 甲组12户家庭用水量统计表
用水量(吨) | 4 | 5 | 6 | 9 |
户数 | 4 | 5 | 2 | 1 |
比较5月份两组家庭用水量的中位数,下列说法正确的是( )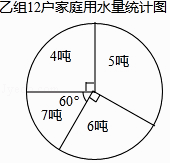
A.甲组比乙组大
B.甲、乙两组相同
C.乙组比甲组大
D.无法判断
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com