练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知长方形ABCD中AB = 8cm，BC = 10cm，在边CD上取一点E，将△ADE折叠，使点D恰好落在BC边上的点F，则CF的长为（ ）

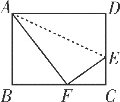
    A. 2cm B. 3cm C. 4cm D. 5cm

    【答案】C

    【解析】由将△ADE折叠使点D恰好落在BC边上的点F可得Rt△ADE≌Rt△AFE，所以AF=10cm．在Rt△ABF中由勾股定理得：AB2+BF2=AF2，已知AB、AF的长可求出BF的长，进而得到结论．

    ∵四边形ABCD是矩形，∴AD=BC=10cm，CD=AB=8cm，根据题意得：Rt△ADE≌Rt△AFE，∴AF=10cm．在Rt△ABF中由勾股定理得：AB2+BF2=AF2，即82+BF2=102，∴BF=6cm，∴CF=BC﹣BF=10﹣6=4（cm）．

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某城市自来水收费实行阶梯水价，收费标准如下表所示：

    月用水量

    不超过12吨的部分

    超过12吨的部分且

    不超过18吨的部分

    超过18吨的部分

    收费标准

    2元/吨

    2.5元/吨

    3元/吨

    （1）某用户四月份用水量为16吨，需交水费为多少元？

    （2）某用户五月份交水费50元，所用水量为多少吨？

    （3）某用户六月份用水量为a吨，需要交水费为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，点D，E分别是AB，AC的中点，连接DE并延长到点F，使EF＝ED，连接CF.

    (1)四边形DBCF是平行四边形吗？说明理由；

    (2)DE与BC有什么样的位置关系和数量关系？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】①下午 2 点 10 分时，钟表的时针和分针所成锐角是________；

    ②如图，射线 OC，OD 在∠AOB 的内部，射线 OM，ON 分别平分∠AOD，∠BOC， 且∠BON=50°，∠AOM=40°，∠COD=30°，则∠AOB 的度数为______．

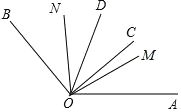
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法中正确的是（ ）

    A. 若|a|=﹣a，则 a 一 定是负数

    B. 单项式 x3y2z 的系数为 1，次数是 6

    C. 若 AP=BP，则点 P 是线段 AB 的中点

    D. 若∠AOC=∠AOB，则射线 OC 是∠AOB 的平分线

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：

    (1)5﹣（﹣3）+（﹣2）﹣1；

    (2)2×（﹣）÷（﹣3）；

    (3)﹣5×[1﹣（0.5+ ）÷]；

    (4)20×（﹣）+4×（﹣）+2×（﹣）；

    (5)﹣14-（）÷（﹣）×[﹣2﹣（﹣3）2]﹣(﹣0.52)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在直线AB上的一点O，以O为端点依次作射线OE，OC，OD，使∠EOD=90°，∠COB=60°

    （1）如图1当∠EOD的一边OD在射线OB上时，求∠COE的度数；

    （2）如图2当∠EOD绕着点O逆时针旋转到OC平分∠BOE时，求∠COD的度数；

    （3）当∠EOD绕着点O逆时针旋转，且O°＜∠AOE＜90°（但≠60°）时，试猜想∠AOE与∠COD有怎样的数量关系，并说明理由．

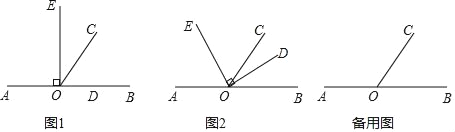
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下列多面体，并把下表补充完整.

    名称

    三棱柱

    四棱柱

    五棱柱

    六棱柱

    图形

    顶点数

    6

    10

    12

    棱数

    9

    12

    面数

    5

    8

    观察上表中的结果，你能发现、、之间有什么关系吗？请写出关系式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】求证：菱形的两条对角线互相垂直． 已知：如图，四边形ABCD是菱形，对角线AC，BD交于点O．
    求证：AC⊥BD．
    以下是排乱的证明过程：
    ①又BO=DO；
    ②∴AO⊥BD，即AC⊥BD；
    ③∵四边形ABCD是菱形；
    ④∴AB=AD．
    证明步骤正确的顺序是（ ）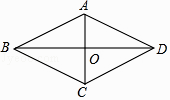

    A.③→②→①→④
    B.③→④→①→②
    C.①→②→④→③
    D.①→④→③→②

    查看答案和解析>>

    同步练习册答案