
 年的维修、保养费用累计为
年的维修、保养费用累计为 (万元),且
(万元),且 ,若第1年的维修、保养费用为2万元,第2年为4万元。
,若第1年的维修、保养费用为2万元,第2年为4万元。 与
与 之间的关系式;
之间的关系式;科目:初中数学 来源:不详 题型:解答题

 x2+bx+c经过B、P两点,求抛物线的解析式;
x2+bx+c经过B、P两点,求抛物线的解析式; 轴的平行线交抛物线于N,求线段MN的最大值.
轴的平行线交抛物线于N,求线段MN的最大值.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
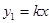 的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数
的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数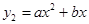 的图象如图②所示.
的图象如图②所示.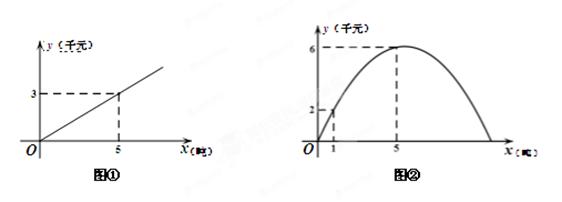
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
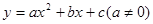 的图象如图所示对称轴为x=-1/2。
的图象如图所示对称轴为x=-1/2。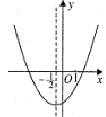
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com