
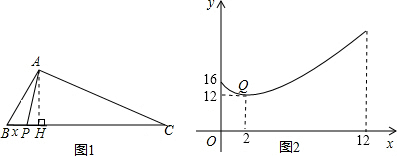
分析 (1)当AP⊥BC时可知AP2最小,由函数图象可知AP2的值,可求得AP的长即AH的长,在△ABH中,利用三角函数定义可求得AB;
(2)当∠APB=90°时,由(1)利用直角三角形的性质可求得BP的长,当∠BAP=90°时,由直角三角形的性质可知BP=2AB,可求得答案.
解答 解:
(1)当AP⊥BC时可知AP2最小,
∵函数图象中过Q点时函数值最小,
∴AH=$\sqrt{12}$=2$\sqrt{3}$,即BC边上的高为2$\sqrt{3}$;
在Rt△ABH中,∠B=60°,
∴$\frac{AH}{AB}$=sin60°,即$\frac{2\sqrt{3}}{AB}$=$\frac{\sqrt{3}}{2}$,解得AB=4,
故答案为:4;2$\sqrt{3}$;
(2)当∠APB=90°时,在△ABP中,∠B=60°,
∴∠BAP=30°,∴BP=$\frac{1}{2}$AB=2;
当∠BAP=90°时,在△ABP中,∠B=60°,
∴∠APB=30°,
∴BP=2AB=8.
综上可知当△ABP为直角三角形时,BP的长是2或8.
点评 本题为二次函数的综合应用,涉及函数图象与性质、三角函数定义、直角三角形的性质及分类讨论思想等知识.在(1)中由图象信息得出AH的长是解题的关键,在(2)中分两种情况分别利用直角三角形的性质求得BP与AB的关系是解题的关键.本题考查知识较基础,较易得分.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 图形 |  |  |  | … |
| 直线条数 | 2 | 3 | 4 | … |
| 最多交点个数 | 1 | 3=1+2 | 6=1+2+3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在一个标准大气压下,加热到100℃,水沸腾 | |
| B. | 抛一枚硬币,正面朝上 | |
| C. | 某运动员射击一次,击中靶心 | |
| D. | 明天一定是晴天 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,∠MON=30°,且OP平分∠MON,过点P作PQ∥OM交ON于点Q.若点P到OM的距离为2,则OQ的长为( )
如图,∠MON=30°,且OP平分∠MON,过点P作PQ∥OM交ON于点Q.若点P到OM的距离为2,则OQ的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
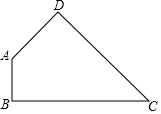 如图,四边形ABCD中,∠ABC=∠ADC=90°,∠C<90°.点E、F分别是BC、CD上的动点,满足:△AEF的周长最小.
如图,四边形ABCD中,∠ABC=∠ADC=90°,∠C<90°.点E、F分别是BC、CD上的动点,满足:△AEF的周长最小.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 3 | 2 | 1 | 0 | -1 | -2 |
| A. | x>0 | B. | x<0 | C. | x>1 | D. | x<1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com