练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．如图，∠MON=30°，且OP平分∠MON，过点P作PQ∥OM交ON于点Q．若点P到OM的距离为2，则OQ的长为（　　）
    A．1B．2C．3D．4

    分析 过P作PF⊥OM，PE⊥ON，根据角平分线的性质得到OE=OF，∠1=∠2，根据平行线的性质得到∠1=∠3，根据直角三角形的性质即可得到结论．

    解答 解：过P作PF⊥OM，PE⊥ON，
    ∵OP平分∠MON，
    ∴OE=OF，∠1=∠2，
    ∵PQ∥OM，
    ∴∠1=∠3，
    ∴∠2=∠3=$\frac{1}{2}$∠MON=15°，
    ∴OQ=PQ，∠4=30°，
    ∴PQ=2PE=4
    ∴OQ=PQ=4．
    故选D．

    点评 本题考查了角平分线的性质，平行线的性质，正确的作出辅助线是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    8．已知x=2017时，代数式ax3+bx-2的值是2，当x=-2017时，代数式ax3+bx+5的值等于（　　）
    A．9B．1C．5D．-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．已知一次函数y=kx-3的图象过点（2，-1），这个函数的解析式为y=x-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

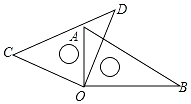    6．如图，将两块直角三角尺的直角顶点O叠放在一起．
    （1）若∠AOD=25°，则∠AOC=65°，∠BOD=65°，∠BOC=155°；
    （2）比较∠AOC与∠BOD的大小关系，并说明理由；
    （3）猜想∠AOD与∠BOC的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．在△ABC中，∠B=60°，点P为BC边上一点，设BP=x，AP2=y（如图1），已知y是x的二次函数的一部分，其图象如图2所示，点Q（2，12）是图象上的最低点．
    （1）边AB=4，BC边上的高AH=2$\sqrt{3}$；
    （2）当△ABP为直角三角形时，BP的长是多少．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．解分式方程：$\frac{x}{x+2}$-1=$\frac{2}{x}$．

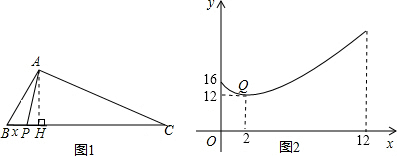
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．两地相距600千米，甲乙两车分别从两地同时出发相向而行，甲车比车乙每小时多走10千米，4小时后两车相遇，则乙车的速度是（　　）
    A．70千米/小时B．75千米/小时C．80千米/小时D．85千米/小时

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

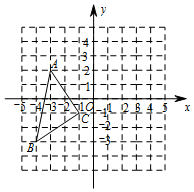    7．如图，（1）画出△ABC先向右平移4个单位，再向上平移1个单位后的图形△A'B'C'；
    （2）求直线A'C'的解析式；
    （3）求△ABC中AB边上的高．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．下列命题中，假命题的是（　　）
    A．三角形中最大的内角不能小于60°
    B．三角形的外角一定大于和它相邻的内角
    C．等边三角形是轴对称图形，它的对称轴有3条
    D．三角形的一条中线把该三角形分成面积相等的两个部分

    查看答案和解析>>

    同步练习册答案