
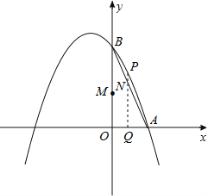
【题目】如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=﹣1.
(1)求抛物线对应的函数关系式;
(2)动点Q从点O出发,以每秒1个单位长度的速度在线段OA上运动,同时动点M从M从O点出发以每秒3个单位长度的速度在线段OB上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒.
①当t为何值时,四边形OMPQ为矩形;
②△AON能否为等腰三角形?若能,求出t的值;若不能,请说明理由.
【答案】解:(1)根据题意,设抛物线的解析式为:![]() ,
,
∵点A(1,0),B(0,3)在抛物线上,
∴![]() ,解得:
,解得:![]() 。
。
∴抛物线的解析式为:![]() 。
。
(2)①∵四边形OMPQ为矩形,
∴OM=PQ,即![]() ,整理得:t2+5t﹣3=0,
,整理得:t2+5t﹣3=0,
解得![]() (
(![]() <0,舍去)。
<0,舍去)。
∴当![]() 秒时,四边形OMPQ为矩形。
秒时,四边形OMPQ为矩形。
②Rt△AOB中,OA=1,OB=3,∴tanA=3。
若△AON为等腰三角形,有三种情况:
(I)若ON=AN,如答图1所示,
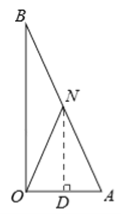
过点N作ND⊥OA于点D,
则D为OA中点,OD=![]() OA=
OA=![]() ,
,
∴t=![]() 。
。
(II)若ON=OA,如答图2所示,
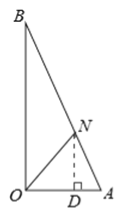
过点N作ND⊥OA于点D,
设AD=x,则ND=ADtanA=3x,OD=OA﹣AD=1﹣x,
在Rt△NOD中,由勾股定理得:OD2+ND2=ON2,
即![]() ,解得x1=
,解得x1=![]() ,x2=0(舍去)。
,x2=0(舍去)。
∴x=![]() ,OD=1﹣x=
,OD=1﹣x=![]() 。
。
∴t=![]() 。
。
(III)若OA=AN,如答图3所示,
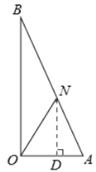
过点N作ND⊥OA于点D,
设AD=x,则ND=ADtanA=3x,
在Rt△AND中,由勾股定理得:ND2+AD2=AN2,
即![]() ,解得x1=
,解得x1=![]() ,x2=
,x2=![]() (舍去)。
(舍去)。
∴x=![]() ,OD=1﹣x=1﹣
,OD=1﹣x=1﹣![]() 。
。
∴t=1﹣![]() 。
。
综上所述,当t为![]() 秒、
秒、![]() 秒,1﹣
秒,1﹣![]() 秒时,△AON为等腰三角形。
秒时,△AON为等腰三角形。
【解析】(1)用待定系数法求出抛物线的顶点式解析式。
(2)①当四边形OMPQ为矩形时,满足条件OM=PQ,据此列一元二次方程求解。
②△AON为等腰三角形时,可能存在三种情形,分类讨论,逐一计算。


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.

(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.
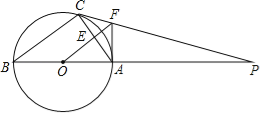
(1)判断AF与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,AF=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.
(1)求甲、乙两种型号的机器人每台的价格各是多少万元;
(2)已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件,该公司计划最多用41万元购买8台这两种型号的机器人,则该公司该如何购买,才能使得每小时的分拣量最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,重庆被“抖音”抖成了“网红城市”,其中解放碑的游客数量明显高于去年同期,如图,小冉和小田决定用所学知识测量解放碑AB的高度,按照以下方式合作并记录所得数据:小冉从大厦DG的底端D点出发,沿直线步行10.2米到达E点,再沿坡度i=1:2.4的斜坡EF行走5.2米到达F点,最后沿直线步行30米到达解放碑底部B点,小田从大厦DG的底端乘直行电梯上行到离D点51.5米的顶端G点,从G点观测到解放碑顶端A点的俯角为26°,若A,B,C,D,E,F,G在同一平面内,且B,F和C,E,D分别在同一水平线上,则解放碑AB的高度约为( )米.(精确到0.1米,参考数据:sin26°≈0.44,cos26°≈.90,tan26°≈0.49)
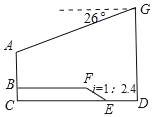
A. 29.0 B. 28.5 C. 27.5 D. 27.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3![]() ,求弦AD的长.
,求弦AD的长.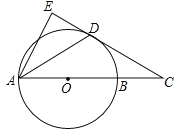
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com