
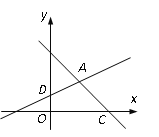
【题目】如图,在平面直角坐标系xOy中,直线y=-x+3与x轴交于点C,与直线AD交于点A(![]() ,
, ![]() ),点D的坐标为(0,1).
),点D的坐标为(0,1).
(1)求直线AD的解析式;
(2)直线AD与x 轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标.
【答案】(1)求直线AD的解析式y=![]() x+1;(2)点E的坐标(2,2)或(3,
x+1;(2)点E的坐标(2,2)或(3, ![]() ).
).
【解析】试题分析:
(1) 利用点A和点D的坐标,结合一次函数的一般形式,通过待定系数法获得关于待定系数的方程,求解这些方程进而可以写出直线AD的解析式.
(2) 根据题意和相似三角形的相关知识可知,本小题应按∠BOD=∠BEC=90°和∠BOD=∠BCE=90°分为两种情况进行讨论. 在第一种情况下,可以过点E作x轴的垂线EF,利用相似三角形的关系,求得线段EC的长,进而在Rt△EFC中利用勾股定理和点E的坐标特征获得相关的方程,求解这一方程即可获得点E的坐标. 在第二种情况下,可以利用EC垂直于x轴的关系直接得到点E的横坐标值,将点E的横坐标代入直线AD的解析式即可得到点E的纵坐标值,进而写出点E的坐标.
试题解析:
(1) 设直线AD的解析式为y=kx+b (k≠0).
将点A和点D的坐标分别代入直线AD的解析式,得
 ,
,
解之,得
 ,
,
∴直线AD的解析式为![]() .
.
(2) 根据题意,分别对下面两种情况进行讨论.

①∠BOD=∠BEC=90°,即△BOD∽△BEC.
如图①,过点E作EF⊥BC,垂足为F.
设点E的坐标为(m, n).
∵点E在直线AD上,
∴![]() .
.
∴点E的坐标为(m, ![]() ).
).
∴OF=m,EF=![]() .
.
∵直线y=-x+3与x轴交于点C,
又∵当y=0时,-x+3=0,即x=3,
∴点C的坐标为(3, 0),
∴OC=3.
同理,点B的坐标为(-2, 0).
∴OB=2.
∴BC=OB+OC=2+3=5.
∵点D的坐标为(0, 1),
∴OD=1.
∴在Rt△BOD中, ![]() .
.
∵△BOD∽△BEC,
∴![]() .
.
∴![]() .
.
∵OF=m,EF=![]() .
.
∴FC=OC-OF=3-m.
∵在Rt△EFC中,EC2=EF2+FC2,
∴![]() ,
,
∴m=2.
∴![]() .
.
∴点E的坐标为(2, 2).
②∠BOD=∠BCE=90°,即△BOD∽△BCE.
设点E的坐标为(m, n).
∵∠BCE=90°,OC=3,
∴m=3.
∵点E在直线AD上,
∴当m=3时, ![]() .
.
∴点E的坐标为(3, ![]() ).
).
综上所述,点E的坐标为(2, 2)或(3, ![]() ).
).


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】2016年末,北京市常住人口2172.9万人,2017年末比上年末减少2.2万人,则2017年末北京市常住人口为( )
A. 2.1707×107人B. 2.1751x107人C. 2.1751×103人D. 2.1707×103人
查看答案和解析>>
科目:初中数学 来源: 题型:
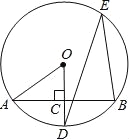
【题目】如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
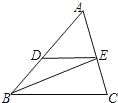
【题目】如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)求证:AEBC=BDAC;
(2)如果![]() =3,
=3,![]() =2,DE=6,求BC的长.
=2,DE=6,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图所示的竖式与横式两种无盖的长方形纸箱.(加工时接缝材料不计)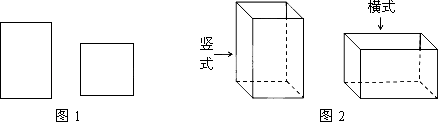
(1)若该厂购进正方形纸板1000张,长方形纸板2000张.问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完;
(2)该工厂某一天使用的材料清单上显示,这天一共使用正方形纸板50张,长方形纸板a张,全部加工成上述两种纸盒,且120<a<136,试求在这一天加工两种纸盒时,a的所有可能值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,不正确的是( )
A.5是25的算术平方根
B.m2n与mn2是同类项
C.多项式﹣3a3b+7ab+1的次数是4
D.﹣8的立方根为﹣2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com