
【题目】如图,在△ABC中,∠ACB=90°,∠A>∠B.
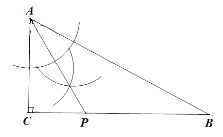
(1)利用尺规作图在BC边上找一点P,使得点P到AB的距离等于PC的长度(不写作法,保留作图痕迹);
(2)在(1)的条件下,如果点P恰好又在线段AB的垂直平分线上,求∠B的度数.
【答案】(1)作图见解析;(2)30°.
【解析】试题分析:(1)因为角平分线上的点到角两边的距离相等,所以要在BC上找一点P,使得点P到AB的距离等于PC的长度,则作角∠BAC的角平分线,角平分线与BC的交点即所求点P,(2)利用垂直平分线的性质可得:PA=PB,所以∠B=∠PAB,又因为(1)中AP是∠BAC的角平分线,所以∠B=∠PAB=![]() ∠BAC,因为∠BAC+∠B=90°,所以3∠B=90°,即∠B=30°.
∠BAC,因为∠BAC+∠B=90°,所以3∠B=90°,即∠B=30°.
试题解析:(1)如图所示,
(2) 因为(1)中AP是∠BAC的角平分线,
所以∠PAB=![]() ∠BAC,即∠BAC=2∠PAB,
∠BAC,即∠BAC=2∠PAB,
又因为点P在线段AB的垂直平分线上,
所以PA=PB,
所以∠B=∠PAB,即∠BAC=2∠B,
又因为∠BAC+∠B=90°,
所以3∠B=90°,即∠B=30°.
点睛:本题主要考查角平分线的性质和垂直平分线的性质,解决本题的关键是能够熟练利用角平分线的性质和垂直平分线的性质.


科目:初中数学 来源: 题型:
【题目】截至2013年末全国大陆总人口约为1360000000人,数字1360000000用科学记数法表示为( )
A.136×107B.13.6×108C.1.36×109D.0.136×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步发展基础教育,自2014年以来,某县加大了教育经费的投入,2014年该县投入教育经费6000万元.2016年投入教育经费8640万元.假设该县这两年投入教育经费的年平均增长率相同.
(1)求这两年该县投入教育经费的年平均增长率;
(2)若该县教育经费的投入还将保持相同的年平均增长率,请你预算2017年该县投入教育经费多少万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
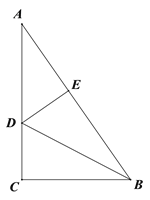
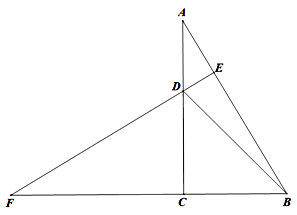
【题目】如图,Rt△ABC中,∠ACB=90°,D为AC上一动点(不与点A、C重合),过D作DE⊥AB于E.
(1)当BD平分∠ABC时
①若AC=8,BC=6,求线段AE的长度;
②在①的条件下,求△ADB的面积;
(2)延长BC、ED相交于点F,若CD=CB,∠CDF=60°,求∠DBE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=![]() +bx+c(a>0)的顶点为P,其图象与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:①m=3;②当∠APB=120°时,a=
+bx+c(a>0)的顶点为P,其图象与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:①m=3;②当∠APB=120°时,a=![]() ;③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;④抛物线上存在点N,当△ABN为直角三角形时,有a≥
;③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;④抛物线上存在点N,当△ABN为直角三角形时,有a≥![]() .正确的是( ).
.正确的是( ).
A.①② B.③④ C.①②③ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
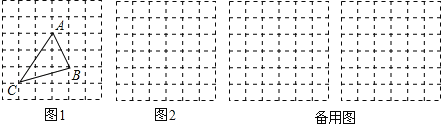
【题目】在△ABC中,AB、BC、AC三边的长分别为![]() ,
, ![]() ,
, ![]() ,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)△ABC的面积为 .
(2)若△DEF的三边DE、EF、DF长分别为![]() ,
, ![]() ,
, ![]() ,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
(3)在△ABC中,AB=2![]() ,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只电子蚂蚁在数轴上从-3出发向左运动2个单位长度到点A处,再向右运动4个单位长度到点C处.
(1)画出数轴标出A、C所表示的数;
(2)这只电子蚂蚁一共运动多少个单位长度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com