
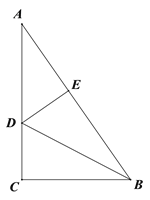
【题目】如图,Rt△ABC中,∠ACB=90°,D为AC上一动点(不与点A、C重合),过D作DE⊥AB于E.
(1)当BD平分∠ABC时
①若AC=8,BC=6,求线段AE的长度;
②在①的条件下,求△ADB的面积;
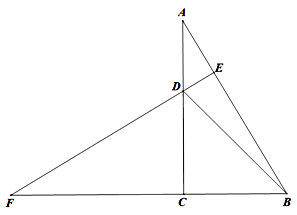
(2)延长BC、ED相交于点F,若CD=CB,∠CDF=60°,求∠DBE的度数.
【答案】(1)① 4;②15;(2)15°.
【解析】试题分析:(1) ①先根据勾股定理求出AB,再根据角平分线的性质可证得:CD=DE,利用HL判定Rt△DCB≌Rt△DEB,所以CB=EB=6,然后根据线段和差关系计算AE的长度,
②设DC=x,则DE= x ,AD=8-x,在Rt△ADE中,利用勾股定理列方程,求出x,可得DE,然后利用三角形面积公式进行计算求△ADB的面积,
(2)根据∠CDF=60°,可得∠ADE=60°,因为DE⊥AB,所以∠DAE=90°-60°=30°,
所以∠ABC=90°-30°=60°,根据角的和差关系可求得∠DBE的度数.
试题解析:(1) ①在Rt△ABC中,AC=8,BC=6,由勾股定理可得:
AB=![]() ,
,
因为BD平分∠ABC, ∠ACB=90°,DE⊥AB,
所以DC=DE,
在Rt△DCB和Rt△DEB中,
![]() ,
,
所以Rt△DCB≌Rt△DEB,
所以EB=CB=6,
所以AE=AB-EB=10-6=4,
②设DC=x,则DE= x ,AD=8-x,
在Rt△ADE中,由勾股定理可得:
![]() ,即
,即![]() ,
,
解得x=3,即DE=3,
所以![]() .
.
(2)因为∠CDF=60°,
所以∠ADE=60°,
因为DE⊥AB,
所以∠DAE=90°-60°=30°,
所以∠ABC=90°-30°=60°,
又因为DC=BC,∠BCD=90°,
所以∠CBD=45°,
所以∠DBE=∠ABC-∠CBD=60°-45°=15°.


科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有2个红球(记为红球1、红球2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
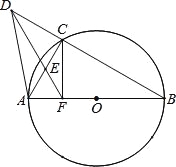
【题目】已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形
(1)求证:△DFB是等腰三角形;
(2)若DA=![]() AF,求证:CF⊥AB.
AF,求证:CF⊥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用反证法证明命题“四边形中至少有一个角是钝角或直角”,应首先假设这个四边形中( )
A.没有一个角是锐角
B.每一个角都是钝角或直角
C.至少有一个角是钝角或直角
D.所有角都是锐角
查看答案和解析>>
科目:初中数学 来源: 题型:
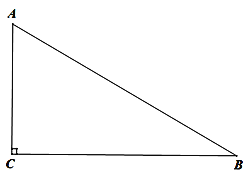
【题目】如图,在△ABC中,∠ACB=90°,∠A>∠B.
(1)利用尺规作图在BC边上找一点P,使得点P到AB的距离等于PC的长度(不写作法,保留作图痕迹);
(2)在(1)的条件下,如果点P恰好又在线段AB的垂直平分线上,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列依次排列的一列数.请接着写出后面的3个数和第10个数.
① 1,-2,1,-2,1,-2, , , ; .
②1, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , , , ; .
, , , ; .
③-2,4,-6,8,-10, , , ; .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com