
����Ŀ��ij�����ƻ�����A��B���ֲ�Ʒ��60�����蹺��ס������ֲ��ϣ�����һ��A��Ʒ����ֲ���4ǧ�ˣ����ֲ���1ǧ�ˣ�����һ��B��Ʒ��ס��������ֲ��ϸ�3ǧ�ˣ������㣬����ס������ֲ��ϸ�1ǧ�˹����ʽ�60Ԫ��������ֲ���2ǧ�˺����ֲ���3ǧ�˹����ʽ�155Ԫ��
��1���ס������ֲ���ÿǧ�˷ֱ��Ƕ���Ԫ��
��2���ֹ������ڹ���ס������ֲ��ϵ��ʽ���9900Ԫ��������B��Ʒ������38�����ʷ������������������������ļ��֣�
��3���ڣ�2���������£�������һ��A��Ʒ��ӹ���40Ԫ��������һ��B��Ʒ��ӹ���50Ԫ��Ӧѡ����������������ʹ������60����Ʒ�ijɱ���ͣ����ɱ�=���Ϸ�+�ӹ��ѣ�
���𰸡���1�����ֲ���ÿǧ��25Ԫ�����ֲ���ÿǧ��35Ԫ����2�������ַ�������3������A��Ʒ22����B��Ʒ38���ɱ����.
�������������������1��(1)��ײ���ÿǧ��xԪ���Ҳ���ÿǧ��yԪ�����ݹ���ס������ֲ��ϸ�1ǧ�˹����ʽ�60Ԫ��������ֲ���2ǧ�˺����ֲ���3ǧ�˹����ʽ�155Ԫ�����г�������![]() �ⷽ���鼴�ɵõ��ײ���ÿǧ��25Ԫ���Ҳ���ÿǧ��35Ԫ��
�ⷽ���鼴�ɵõ��ײ���ÿǧ��25Ԫ���Ҳ���ÿǧ��35Ԫ��
��2��������A��Ʒm��,����B��Ʒ(60m)������������60����Ʒ�IJ��Ϸ�Ϊ:
25��4m+35��1m+25��3(60m)+35��3(60m)=45m+10800�����ݹ���ס������ֲ��ϵ��ʽ���9900Ԫ�õ�![]() ��������B��Ʒ������38���õ�
��������B��Ʒ������38���õ�![]() Ȼ�����������ʽ����乫�����ֵõ�
Ȼ�����������ʽ����乫�����ֵõ�![]() ��
��![]() ��������
Ϊ��������![]() ��ֵΪ20��21��22���÷�������������������
��ֵΪ20��21��22���÷�������������������
��3��������A��Ʒm��,�������ɱ�ΪWԪ,�ӹ���Ϊ��40m+50(60m)�����ݳɱ�=���Ϸ�+�ӹ��ѵõ�W=45m+10800+40m+50(60m)=55m+13800������һ�κ��������ʵõ�W��m���������С��Ȼ���![]() =22���룬���ɵõ���ͳɱ�������������
=22���룬���ɵõ���ͳɱ�������������
���������(1)��ײ���ÿǧ��xԪ���Ҳ���ÿǧ��yԪ��
��![]() ���
���![]()
���Լײ���ÿǧ��25Ԫ���Ҳ���ÿǧ��35Ԫ��
(2)������A��Ʒm��,����B��Ʒ(60m)������������60����Ʒ�IJ��Ϸ�Ϊ:
25��4m+35��1m+25��3(60m)+35��3(60m)=45m+10800��
�����⣺ ![]() ���
���![]()
��![]() ���
���![]()
![]()
��m��ֵΪ20��21��22��
�������ַ�����
������A��Ʒ20��������B��Ʒ40����
������A��Ʒ21��������B��Ʒ39����
������A��Ʒ22��������B��Ʒ38����
(3)������A��Ʒm��,�������ɱ�ΪWԪ,�ӹ���Ϊ��40m+50(60m)��
��W=45m+10800+40m+50(60m)=55m+13800��
��55<0��
��W��mspan>�����������
��m=20��21��22��
�൱m=22ʱ���ܳɱ���͡�
��ѡ������A��Ʒ22��������B��Ʒ38�����ܳɱ����.


 �������ͬ������ϵ�д�
�������ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC��ƽ��ֱ������ϵxOy�е�λ����ͼ��ʾ��

��1������ABC���ڵ�C�����ĶԳƵ���A1B1C1��
��2������A1B1C1����ƽ��4����λ������ƽ�ƺ����A2B2C2��
��3����x��������һ��P��ʹPA1+PC2��ֵ��С����д����P�����꣨��д�����̣�ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ��������֣�����������Ϣ����������⣺�Ѽ������ô��������������м��ö��Ÿ������磺{3��4}��{��3��6��8��18}�����д������ڵ�������Ϊ���ϵ�Ԫ�أ����һ���������㣺ֻҪ������һ��Ԫ��a��ʹ�é�2a+4Ҳ��������ϵ�Ԫ�أ������ļ��ϳ�Ϊ�������ϣ����磻{3����2}����Ϊ��2��3+4����2����2ǡ����������ϵ�Ԫ��������{3����2}���������ϣ����磻����2��9��8��}����Ϊ��2������2��+4��8��8ǡ����������ϵ�Ԫ�أ�����{��2��9��8��}���������ϣ�
��1������{��4��12}�Ƿ����������ϣ�
��2������{![]() ����
����![]() ��
��![]() }�Ƿ����������ϣ�
}�Ƿ����������ϣ�
��3��������{8��n}��{m}�����������ϣ���m��n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̥��ֱ���Ƿ���ϱ������ж���̥�����ĺ�������Ҫ����֮һ��������̥��ij����̥�ı�ֱ����600mm����������Ա��������Ʒ�г�ȡ10����̥���м�飬������ֱ���ĺ�������Ϊ��������ĺ�������Ϊ��������¼���£���λ��mm����
��� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
����� |
|
|
| 0 |
|
|
|
|
|
|
��
��2������10����̥��ƽ��ֱ������ȷ��![]() mm����
mm����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������y= ![]() (x>0)��ͼ�������OABC�ı�BC���ڵ�D���ֱ����A��D��AF��DE����ֱ��y=k2x(k2<0)�ڵ�F��E.��OE=OF��BD=2CD���ı���ADEF�����Ϊ12����k1��ֵΪ________.
(x>0)��ͼ�������OABC�ı�BC���ڵ�D���ֱ����A��D��AF��DE����ֱ��y=k2x(k2<0)�ڵ�F��E.��OE=OF��BD=2CD���ı���ADEF�����Ϊ12����k1��ֵΪ________.
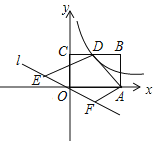
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�FΪAD���е㣬DE��![]() ��CF��BD�ֱ�BD��AD�ڵ�E��F������BF.
��CF��BD�ֱ�BD��AD�ڵ�E��F������BF.
��1����֤��EC��2EF��
��2�����ı���BCDF�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������м�������
�����ڵ������Ƕ��������ı�����ƽ���ı��Σ���һ��Ա�ƽ��һ��Խ���ȵ��ı�����ƽ���ı��Σ���һ��Ա�ƽ����һ��Ա���ȵ��ı�����ƽ���ı��Σ�����һ���Խ���ƽ��һ��Խǵ��ı��������Σ��ݶԽ�������һ��ഹֱ���ı�����������.
A. 1��B. 2��
C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����������ABCD��ȡһ��E������AE��BE��DE������A��AE�Ĵ��߽�DE�ڵ�P����AE=AP=1��PB=![]() �����н��ۣ��١�APD�ա�AEB���ڵ�B��ֱ��AE�ľ���Ϊ
�����н��ۣ��١�APD�ա�AEB���ڵ�B��ֱ��AE�ľ���Ϊ![]() ����EB��ED����S��APD+S��APB=1+
����EB��ED����S��APD+S��APB=1+![]() ����S������ABCD=4+
����S������ABCD=4+![]() ��������ȷ���۵�����ǣ� ��
��������ȷ���۵�����ǣ� ��

A.�٢ۢ� B���٢ڢ� C���ۢܢ� D���٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC=6����BAC=120����AΪ����ĵĵȱ�������ADE�Ƶ�A�ڡ�BAC����ת��AD��AE��BC�߷ֱ��ڵ�F��G����B����ֱ��AD�ĶԳƵ�ΪM��MG��BC����BF�ij�Ϊ____________.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com