
【题目】如图,在△ABC中,AB=AC=6,∠BAC=120,以A为顶点的的等边三角形ADE绕点A在∠BAC内旋转,AD、AE与BC边分别交于点F、G若点B关于直线AD的对称点为M,MG⊥BC,则BF的长为____________.

【答案】![]()
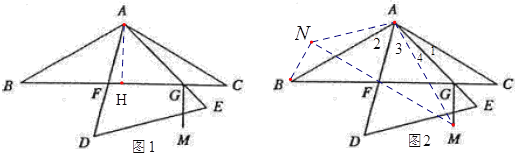
【解析】作AH⊥BC于H,如图1,
∵AB=AC=6,∠BAC=120°,
∴∠B=30°,BH=CH,
在Rt△ABH中,AH=![]() AB=3,BH=
AB=3,BH=![]() AH=3
AH=3![]() ,,
,,
∴BC=2BH=6![]() ,
,
把△ACG绕点A顺时针旋转120°得到△ABN,连结FN、AM,FM,如图2,
则BN=CG,AG=AG,∠ABN=∠C=30°,∠1=∠BAN,
∴∠FBN=60°,
∵∠FAG=60°,
∴∠1+∠2=60°,
∴∠FAN=60°,
在△AFG和△AFN中, 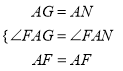 ,
,
∴△AFG≌△AFN,
∴FG=FN,
∵点B关于直线AD的对称点为M,
∴FB=FM,AB=AM,∠2=∠3,
而∠3+∠4=60°,∠1+∠2=60°,
∴∠1=∠4,
而AC=AB=AM,
∴△AMG与△ACG关于AG对称,
∴GM=GC,
∴GM=BN,
在△FMG和△FBN中, 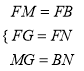 ,
,
∴△FMG≌△FBN,
∴∠FGM=∠BNF=90°,
在Rt△BFN中,∵∠FBN=60°,∴BN=![]() BF,FN=
BF,FN=![]() BF,
BF,
∴CG=![]() BF,FG=
BF,FG=![]() BF,
BF,
∴BF+![]() BF+
BF+![]() BF=BC=6
BF=BC=6![]() ,
,
∴BF=6![]() -6,
-6,
故答案为:6![]() -6.
-6.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料.生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产B产品不少于38件,问符合生产条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择那种生产方案,使生产这60件产品的成本最低?(成本=材料费+加工费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,格点三角形![]() (顶点为网格线的交点)的顶点
(顶点为网格线的交点)的顶点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.

(1)请在网格图中建立平面直角坐标系;
(2)将![]() 先向左平移5个单位长度,再向下平移6个单位长度,请画出两次平移后的
先向左平移5个单位长度,再向下平移6个单位长度,请画出两次平移后的![]() ,并直接写出点
,并直接写出点![]() 的对应点
的对应点![]() 的坐标;
的坐标;
(3)若![]() 是
是![]() 内一点,直接写出
内一点,直接写出![]() 中的对应点
中的对应点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)45+(-20)
(2)(-8)-(-1)
(3)|-10|+|+8|
(4)![]()
(5)![]()
(6)![]()
(7)![]()
(8)![]()
(9)![]()
(10)![]()
(11)![]()
(12)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一出租车一天下午以鼓楼为出发点在东西方向运营,向东走为正,向西走为负,行车里程(单位:km)依先后次序记录如下:![]() .
.
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,如图,△ABC和△DEF是两个边长为10cm的等边三角形,且点B、D、C、E在同一直线上连接AD、CF.若BD=4cm,△ABC沿着BE的方向以2cm/s的速度运动,设△ABC运动时间为ts,当t为何值时,四边形ADFC是菱形?请说明你的理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(n,3),B(-3,-2)两点.
的图象交于A(n,3),B(-3,-2)两点.
(1)求反比例函数与一次函数的解析式;
(2)过点B作BC⊥x轴,垂足为C,求S△ABC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若点P(a,b)在函数y=![]() 的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=
的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=![]() 的一个“派生函数”.例如:点(2,
的一个“派生函数”.例如:点(2, ![]() )在函数y=
)在函数y=![]() 的图象上,则函数y=2x2+
的图象上,则函数y=2x2+ ![]() 称为函数y=
称为函数y=![]() 的一个“派生函数”.现给出以下两个命题:
的一个“派生函数”.现给出以下两个命题:
(1)存在函数y=![]() 的一个“派生函数”,其图象的对称轴在y轴的右侧
的一个“派生函数”,其图象的对称轴在y轴的右侧
(2)函数y=![]() 的所有“派生函数”的图象都经过同一点,下列判断正确的是( )
的所有“派生函数”的图象都经过同一点,下列判断正确的是( )
A. 命题(1)与命题(2)都是真命题
B. 命题(1)与命题(2)都是假命题
C. 命题(1)是假命题,命题(2)是真命题
D. 命题(1)是真命题,命题(2)是假命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com