
【题目】如图,如图,△ABC和△DEF是两个边长为10cm的等边三角形,且点B、D、C、E在同一直线上连接AD、CF.若BD=4cm,△ABC沿着BE的方向以2cm/s的速度运动,设△ABC运动时间为ts,当t为何值时,四边形ADFC是菱形?请说明你的理由

【答案】当t=2时,四边形ADFC是菱形,理 由 见 解 析
【解析】
由△ABC和△FDE都是边长为10cm的等边三角形可得AC=DF,∠ACD=∠FDE=60°,根据平行线的判定定理可得AC∥DF,由此可得四边形ADFC是平行四边形由四边形ADFC是平行四边形,要得到四边形ADFC是菱形,只要邻边相等即可,根据邻边相等可得B与D重合,由此便不难得到t的值.
∵△ABC和△FDE都是边长为10cm的等边三角形,
∴AC=DF,∠ACD=∠FDE=60°
∴AC∥DF
∴四边形ADFC是平行四边形
要使四边形ADFC是矩形,根据四边形ADFC是平行四边形可知只要AC=AD即可
∵AB=AC
∴AD=AB,此时点B与点D重合
∵△ABC沿着BE的方向以2cm/s的速度运动,
∴运动时间t=![]() =2,
=2,
∴当t=2时,四边形ADFC是菱形


科目:初中数学 来源: 题型:
【题目】下列命题中假命题有
①相邻的两个角都互补的四边形是平行四边形;②一组对边平行一组对角相等的四边形是平行四边形;③一组对边平行另一组对边相等的四边形是平行四边形;④有一条对角线平分一组对角的四边形是菱形;⑤对角线相等且互相垂直的四边形是正方形.
A. 1个B. 2个
C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正常情况下,一个人在运动时所能承受的每分钟心跳的最高次数y(次/分)是这个人年龄x(岁)的一次函数。
(1)根据图中信息,求在正常情况下,y关于x的函数关系式;
(2)若一位63岁的人在跑步,医生在途中给他测得10秒心跳为26次,问:他是否有危险?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=6,∠BAC=120,以A为顶点的的等边三角形ADE绕点A在∠BAC内旋转,AD、AE与BC边分别交于点F、G若点B关于直线AD的对称点为M,MG⊥BC,则BF的长为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在数轴上分别表示有理数![]() 、
、![]() ,在数轴上A、B两点之间的距离
,在数轴上A、B两点之间的距离![]() .
.

回答下列问题:
(1)数轴上表示1和![]() 的两点之间的距离是 ;
的两点之间的距离是 ;
(2)数轴上表示![]() 和
和![]() 的两点之间的距离表示为 ;
的两点之间的距离表示为 ;
(3)若![]() 表示一个有理数,请你结合数轴求
表示一个有理数,请你结合数轴求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边AD,AB的长分别为3,8,且B,C在x轴的负半轴上,E是DC的中点,反比例函数y=![]() (x<0)的图象经过点E,与AB交于点F.
(x<0)的图象经过点E,与AB交于点F.
(1)若点B坐标为(﹣6,0),求m的值;
(2)若AF﹣AE=2.且点E的横坐标为a.则点F的横坐标为 (用含a的代数式表示),点F的纵坐标为 ,反比例函数的表达式为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
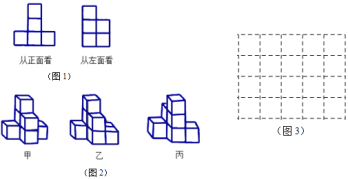
【题目】一个由若干小正方形堆成的几何体,它从正面看和从左面看的图形如图1所示.
![]() 这个几何体可以是图2中甲,乙,丙中的______;
这个几何体可以是图2中甲,乙,丙中的______;
![]() 这个几何体最多由______个小正方体堆成,最少由______个小正方体堆成;
这个几何体最多由______个小正方体堆成,最少由______个小正方体堆成;
![]() 请在图3中用阴影部分画出符合最少情况时的一个从上面往下看得到的图形.
请在图3中用阴影部分画出符合最少情况时的一个从上面往下看得到的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=40海里,某船从港口A出发,沿北偏东15°方向航行半小时后到达B处,此时从观测站O处测得该船位于北偏东60°的方向.求该船航行的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2,BC=4,P为矩形边上的一个动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以A,P,B为顶点的三角形面积为y,则选项图象能大致反映y与x的函数关系的是( )
A. 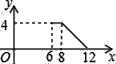 B.
B. 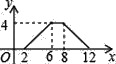 C.
C. 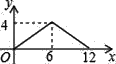 D.
D. 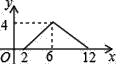
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com