
【题目】如图,点A、B在数轴上分别表示有理数![]() 、
、![]() ,在数轴上A、B两点之间的距离
,在数轴上A、B两点之间的距离![]() .
.

回答下列问题:
(1)数轴上表示1和![]() 的两点之间的距离是 ;
的两点之间的距离是 ;
(2)数轴上表示![]() 和
和![]() 的两点之间的距离表示为 ;
的两点之间的距离表示为 ;
(3)若![]() 表示一个有理数,请你结合数轴求
表示一个有理数,请你结合数轴求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ; (3)最小值:
; (3)最小值:![]() .
.
【解析】
试题(1)|1﹣(﹣3)|=4;
(2)根据在数轴上A、B两点之间的距离AB=|a﹣b|,即可求解;
(3)先去掉绝对值号,然后计算即可得解.
试题解析:(1)|1﹣(﹣3)|=4;
故答案为:4;
(2)|x﹣(﹣3)|=|x+3|;
故答案为:|x+3|;
(3)当x<﹣3时,|x﹣1|+|x+3|=1﹣x﹣x﹣3=﹣2x﹣2,
当﹣3≤x≤1时,|x﹣1|+|x+3|=1﹣x+x+3=4,
当x>1时,|x﹣1|+|x+3|=x﹣1+x+3=2x+2,
在数轴上|x﹣1|+|x+3|的几何意义是:表示有理数x的点到﹣3及到1的距离之和,所以当﹣3≤x≤1时,它的最小值为4.


科目:初中数学 来源: 题型:
【题目】(1)图①表内的各横行中,从第二个数起的数都比它左边相邻的数大m;各竖列中, 从第二个数起的数都比它上边相邻的数大n.请你仔细观察表格,耐心寻找规律, 根据你得到的规律填空:
①m =______;②n =______;③x =______;④y =______;
(2)若(1)题中的规律不变,把表①中的-1,8和y都去掉,如图②,则x=_______(用含m,n的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图所示(1<x=h<2,0<xA<1),下列结论:① 2a+b>0;② abc<0;③ 若OC=2OA,则2b-ac = 4;④ 3a﹣c<0,其中正确的个数是( )
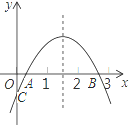
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)45+(-20)
(2)(-8)-(-1)
(3)|-10|+|+8|
(4)![]()
(5)![]()
(6)![]()
(7)![]()
(8)![]()
(9)![]()
(10)![]()
(11)![]()
(12)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC与Rt△ABD中,![]() ,
,![]() ,AC、BD相交于点G,过点A作
,AC、BD相交于点G,过点A作![]() 交CB的延长线于点E,过点B作
交CB的延长线于点E,过点B作![]() 交DA的延长线于点F,AE、BF相交于点H.
交DA的延长线于点F,AE、BF相交于点H.

(1)证明:ΔABD≌△BAC.
(2)证明:四边形AHBG是菱形.
(3)若AB=BC,证明四边形AHBG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,如图,△ABC和△DEF是两个边长为10cm的等边三角形,且点B、D、C、E在同一直线上连接AD、CF.若BD=4cm,△ABC沿着BE的方向以2cm/s的速度运动,设△ABC运动时间为ts,当t为何值时,四边形ADFC是菱形?请说明你的理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:b是最小的正整数,且a、b满足![]() .
.
(1)请求出a、b、c的值;
(2)a、b、c所对应的点分别为A、B、C,点P为动点,其对应的数为x,点P在-1到1之间运动时(即![]() ),请化简式子:
),请化简式子:![]() (写出化简过程);
(写出化简过程);
(3)在(1)、(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒一个单位长度的速度向左运动,同时点B以每秒2个单位长度,点C以每秒5个单位长度的速度向右运动3秒钟后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请求BC-AB的值.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自学下面材料后,解答问题
分母中含有未知数的不等式叫做分式不等式,如:![]() ;
;![]() 等
等![]() 那么如何求出它们的解集呢?
那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负![]() 其字母表达式为:
其字母表达式为:
![]() 若
若![]() ,
,![]() ,则
,则![]() ;若
;若![]() ,
,![]() ,则
,则![]()
![]() 若
若![]() ,
,![]() ,则
,则![]() ;若
;若![]() ,
,![]() ,则
,则![]()
反之:![]() 若
若![]() ,则
,则![]() 或
或![]()
![]() 若
若![]() ,则______或______.
,则______或______.
根据上述规律
![]() 求不等式
求不等式![]() 的解集.
的解集.
![]() 直接写出一个解集为
直接写出一个解集为![]() 或
或![]() 的最简分式不等式.
的最简分式不等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),一架云梯AB斜靠在一竖直的墙上,云梯的顶端A距地面15米,梯子的长度比梯子底端B离墙的距离大5米.
(1)这个云梯的底端B离墙多远?
(2)如图(2),如果梯子的顶端下滑了8m(AC的长),那么梯子的底部在水平方向右滑动了多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com