
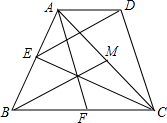
 如图,在四边形ABCD中,AD∥BC,AD=$\frac{1}{2}$BC,AF、BH、CE为△ABC的三条中线,若S四边形ABCD=2,求以AF、BH、CE为边长的三角形面积.小明认为连接DE,则△DEC的面积就是以AF、BH、CE为边长的三角形面积.小明的想法对吗?请说明你的理由,并且求出AF、BH、CE为边长的三角形面积.
如图,在四边形ABCD中,AD∥BC,AD=$\frac{1}{2}$BC,AF、BH、CE为△ABC的三条中线,若S四边形ABCD=2,求以AF、BH、CE为边长的三角形面积.小明认为连接DE,则△DEC的面积就是以AF、BH、CE为边长的三角形面积.小明的想法对吗?请说明你的理由,并且求出AF、BH、CE为边长的三角形面积. 分析 连接EH、DH,先证明四边形AFCD是平行四边形,得出AF=CD,再证明EH是△ABC的中位线,由三角形中位线定理得出EH∥BC,EH=$\frac{1}{2}$BC,证出四边形AEHD是平行四边形,得出AE∥DH,AE=DH,因此BE∥DH,BE=DH,证明四边形BHDE是平行四边形,得出BH=DE,得出△DEC的面积就是以AF、BH、CE为边长的三角形面积,小明的想法对;延长DE交CB的延长线于G,由AAS证明△BEG≌△AED,得出对应边相等GE=DE,△BEG的面积=△AED的面积,得出△DEC的面积=△GEC的面积=$\frac{1}{2}$△DGC的面积,△DGC的面积=四边形ABCD的面积,即可得出结果.
解答 解:小明的想法对;理由如下: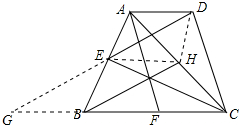
连接EH、DH,如图所示:
∵AF是BC的中线,
∴CF=$\frac{1}{2}$BC,
∵AD∥BC,AD=$\frac{1}{2}$BC,
∴AD=CF,AD∥CF,
∴四边形AFCD是平行四边形,
∴AF=CD,
∵BH、CE为△ABC的中线,
∴EH是△ABC的中位线,AE=BE,
∴EH∥BC,EH=$\frac{1}{2}$BC,
∴AD∥EH,AD=EH,
∴四边形AEHD是平行四边形,
∴AE∥DH,AE=DH,
∴BE∥DH,BE=DH,
∴四边形BHDE是平行四边形,
∴BH=DE,
∴△DEC的面积就是以AF、BH、CE为边长的三角形面积,
延长DE交CB的延长线于G,
∵AD∥BC,
∴∠G=∠ADE,
在△BEG和△AED中,$\left\{\begin{array}{l}{∠G=∠ADE}&{\;}\\{∠BEG=∠AED}&{\;}\\{BE=AE}&{\;}\end{array}\right.$,
∴△BEG≌△AED(AAS),
∴GE=DE,△BEG的面积=△AED的面积,
∴△DEC的面积=△GEC的面积=$\frac{1}{2}$△DGC的面积,
△DGC的面积=四边形ABCD的面积,
∴AF、BH、CE为边长的三角形面积=$\frac{1}{2}$S四边形ABCD=1.
点评 本题的面积及等积变换综合题目,考查了平行四边形的判定与性质、全等三角形的判定与性质、三角形中位线定理、三角形的中线性质、三角形的面积关系等知识;本题综合性强,难度较大,需要通过作辅助线,多次证明四边形是平行四边形才能得出结果.


科目:初中数学 来源: 题型:选择题
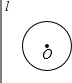 如图,⊙O的圆心O到直线m的距离为3cm,⊙O的半径为1cm,将直线m向右(垂直于m的方向)平移,使m与⊙O相切,则平移的距离为( )
如图,⊙O的圆心O到直线m的距离为3cm,⊙O的半径为1cm,将直线m向右(垂直于m的方向)平移,使m与⊙O相切,则平移的距离为( )| A. | 1cm | B. | 2cm | C. | 4cm | D. | 2cm或4cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
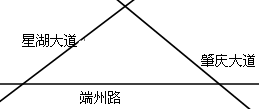 作图:如图,端州区肇庆大道、星湖大道和端州路两两相交,现要在肇庆大道上建一油站,要求油站到星湖大道、端州路的距离相等,请用圆规、直尺作图,在肇庆大道上找出建油站的地点P.
作图:如图,端州区肇庆大道、星湖大道和端州路两两相交,现要在肇庆大道上建一油站,要求油站到星湖大道、端州路的距离相等,请用圆规、直尺作图,在肇庆大道上找出建油站的地点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com