
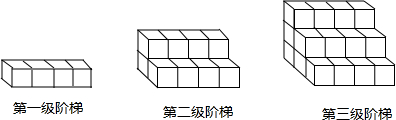
���� ��1����������������ʱ������������Сľ��¶������ı�������㼴�ɣ�
��2�������һ�㣬���ݣ�1���ҵ���ʾ����������Сľ��¶������������θ�����ͨʽ���ɣ�
��� �⣺��1�������������ʱ������������Сľ��¶������������θ�����4��3��3+2��1+2+3��=48��������������Сľ��¶������ı����Ϊ��48��4=192��cm2����
��2�����n������ʱ������������Сľ��¶������������θ�����4��3��n+2��1+2+3+��+n��=12n+n��n+1��=n2+13n������������Сľ��¶������ı����Ϊ����n2+13n����4=4n2+52n��cm2����
���� ������Ҫ����ѧ����ͼ�α仯���������������գ���������Ŀ�Ĺؼ��Ǹ�����Ŀ�и�����ͼ�Ρ���ֵ�����ݵ�����������������ҵ����ɣ�������Ŀ�Ѷ����У������е��⣮


 ��������������������ϵ�д�
��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
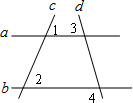 ��ͼ��ֱ��a��b��ֱ��c��d�ཻ������1=��2����3=70�㣬��4�Ķ���Ϊ��������
��ͼ��ֱ��a��b��ֱ��c��d�ཻ������1=��2����3=70�㣬��4�Ķ���Ϊ��������| A�� | 35�� | B�� | 70�� | C�� | 90�� | D�� | 110�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
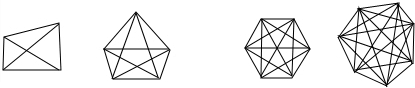
| A�� | p��m��n��q | B�� | m��p��q��n | C�� | m��p��n��q | D�� | p��m��q��n |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
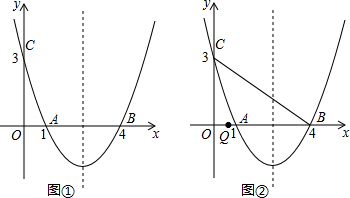
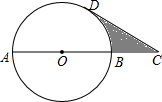 ��ͼ��ABΪ��O��ֱ������C��AB���ӳ����ϣ���AB=2BC=4��CD���O�����ڵ�D����ͼ����Ӱ���ֵ������2$\sqrt{3}$-$\frac{2}{3}$�У�������������źͦУ�
��ͼ��ABΪ��O��ֱ������C��AB���ӳ����ϣ���AB=2BC=4��CD���O�����ڵ�D����ͼ����Ӱ���ֵ������2$\sqrt{3}$-$\frac{2}{3}$�У�������������źͦУ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com