
【题目】如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC= ![]() ,则四边形MABN的面积是( )
,则四边形MABN的面积是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:连接CD,交MN于E, ∵将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,
∴MN⊥CD,且CE=DE,
∴CD=2CE,
∵MN∥AB,
∴CD⊥AB,
∴△CMN∽△CAB,
∴ ![]() ,
,
∵在△CMN中,∠C=90°,MC=6,NC= ![]() ,
,
∴S△CMN= ![]() CMCN=
CMCN= ![]() ×6×2
×6×2 ![]() =6
=6 ![]() ,
,
∴S△CAB=4S△CMN=4×6 ![]() =24
=24 ![]() ,
,
∴S四边形MABN=S△CAB﹣S△CMN=24 ![]() ﹣6
﹣6 ![]() =18
=18 ![]() .
.
故选C.
首先连接CD,交MN于E,由将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,即可得MN⊥CD,且CE=DE,又由MN∥AB,易得△CMN∽△CAB,根据相似三角形的面积比等于相似比的平方,相似三角形对应高的比等于相似比,即可得 ![]() ,又由MC=6,NC=
,又由MC=6,NC= ![]() ,即可求得四边形MABN的面积.
,即可求得四边形MABN的面积.


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
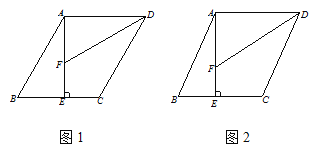
【题目】已知在□ABCD中,AEBC于E,DF平分ADC 交线段AE于F.
(1)如图1,若AE=AD,ADC=60, 请直接写出线段CD与AF+BE之间所满足的等量关系;
(2)如图2, 若AE=AD,你在(1)中得到的结论是否仍然成立, 若成立,对你的结论加以证明, 若不成立, 请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中, ![]() ,
,![]() ;
;![]() 是
是![]() 向右平移5个单位向上平移4个单位之后得到的图象
向右平移5个单位向上平移4个单位之后得到的图象
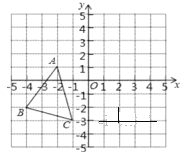
(1)![]() 两点的坐标分别为
两点的坐标分别为![]() ______________
______________![]() ______________.
______________.
(2)作出![]() 平移之后的图形
平移之后的图形![]() .
.
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,小正方形的顶点叫做格点,△ABC叫做格点三角形(三角形的顶点都是格点),请按要求完成:
(1)先将△ABC竖直向上平移6个单位,再水平向右平移3个单位得到△A1B1C1,请在网格中画出△A1B1C1;
(2)将△A1B1C1绕点B1顺时针旋转90°,得到△A2B1C2,请在网格中画出△A2B1C2;
(3)将△ABC沿直线B1 C2翻折,得到△A3B3C,请在网格中画出△A3B3C;
(4)线段BC沿着由B到B1的方向平移至线段B1C1,求线段BC扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,那么在下列各条件中,不能判定Rt△ABC≌Rt△A′B′C′的是( )

A. AB=A′B′=5,BC=B′C′=3 B. AB=B′C′=5,∠A=∠B′=40°
C. AC=A′C′=5,BC=B′C′=3 D. AC=A′C′=5,∠A=∠A′=40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一次函数y=3x﹣2的图象与某反比例函数的图象的一个公共点的横坐标为1.
(1)求该反比例函数的解析式;
(2)将一次函数y=3x﹣2的图象向上平移4个单位,求平移后的图象与反比例函数图象的交点坐标;
(3)请直接写出一个同时满足如下条件的函数解析式: ①函数的图象能由一次函数y=3x﹣2的图象绕点(0,﹣2)旋转一定角度得到;
②函数的图象与反比例函数的图象没有公共点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有如下命题,其中假命题有( ).
①负数没有平方根;
②同位角相等;
③对顶角相等;
④如果一个数的立方根是这个数本身,那么这个数是0.
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品的标志图案如图(1)所示,要在所给的图3-122(2)中,把A,B,C三个菱形通过一种或几种变换,使之变为与图(1)一样的图案.
(1)请你在图3-122(2)中作出变换后的图案;(最终图案用实线)
(2)你所用的变换方法是_________.(填序号)
①将菱形B向上平移;②将菱形B绕点O顺时针旋转120°;③将菱形B绕点O旋转180.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com