
����Ŀ����֪��һ�κ���y=3x��2��ͼ����ij������������ͼ���һ��������ĺ�����Ϊ1��
��1����÷����������Ľ���ʽ��
��2����һ�κ���y=3x��2��ͼ������ƽ��4����λ����ƽ�ƺ��ͼ���뷴��������ͼ��Ľ������ꣻ
��3����ֱ��д��һ��ͬʱ�������������ĺ�������ʽ�� �ٺ�����ͼ������һ�κ���y=3x��2��ͼ���Ƶ㣨0����2����תһ���Ƕȵõ���
�ں�����ͼ���뷴����������ͼ��û�й����㣮
���𰸡�
��1���⣺��x=1����y=3x��2����y=1��
�跴���������Ľ���ʽΪ ![]() ��
��
��x=1��y=1����ã�k=1��
��÷����������Ľ���ʽΪ ![]()
��2���⣺ƽ�ƺ��ͼ���Ӧ�Ľ���ʽΪy=3x+2��
�ⷽ���� 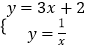 ����
���� ![]() ��
�� ![]() ��
��
��ƽ�ƺ��ͼ���뷴��������ͼ��Ľ�������Ϊ�� ![]() ��3���ͣ���1����1��
��3���ͣ���1����1��
��3���⣺y=��2x��2��
�����ۿ��ţ�������Ϊ��2��һ����ϵ��С�ک�1��һ�κ������ɣ�
����������1��������������Ľ������꣬���ô���ϵ����������÷����������Ľ���ʽ����2��ƽ�ƺ��ͼ���Ӧ�Ľ���ʽΪy=3x+2����������������ʽ��������ý������ꣻ��3��������Ϊ��2��һ����ϵ��С�ک�1��һ�κ������ɣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ӭ��֣���еڶ��조�г�����������У����������ijѧУ��֯��һ������֪ʶ������ÿ��ѡ25��ͬѧ�μӱ������ɼ��ֱ�ΪA��B��C��D�ĸ��ȼ���������Ӧ�ȼ��÷����μ�Ϊ100�֡�90�֡�80�֡�70�֣�ѧУ�����꼶һ��Ͷ���ijɼ����������Ƴ�ͳ��ͼ����ͼ��ʾ��
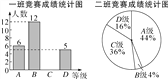
(1)��һ�ྺ���ɼ�ͳ��ͼ����������
(2)д���±���a��b��c��ֵ��
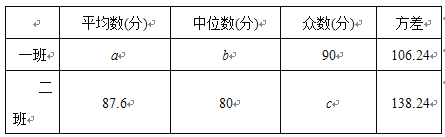
(3)����(2)�Ľ�����������ξ����ɼ��Ľ�����з�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ��߸�CD�ϵ�C��������CE��CF�̶����߸ˣ�����CE�͵������ɵĽǡ�CED=60�㣬������߸�6��B�����ø�Ϊ1.5�IJ����AB����A����õ��߸���C��������Ϊ30�㣬������CE�ij����������С�����һλ���ο����ݣ� ![]() ��1.41��
��1.41�� ![]() ��1.73����
��1.73����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬����ABC��ֱ��MN���ۺ���Cǡ������AB���ϵĵ�D������֪MN��AB��MC=6��NC= ![]() �����ı���MABN������ǣ� ��
�����ı���MABN������ǣ� �� 
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�������з��̣��� ![]() ����
���� ![]() ����
���� ![]() ���������������̺��Ĺ��ɣ������x�ķ���
���������������̺��Ĺ��ɣ������x�ķ��� ![]() ��nΪ���������ĸ�����Ĵ��ǣ� ��
��nΪ���������ĸ�����Ĵ��ǣ� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������A����2��n����x���ϣ����B��n+1��n��1���ڣ� ��
A.��һ����B.�ڶ�����C.��������D.��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� 
��1����ͼ��1����������AEGH�Ķ���E��H��������ABCD�ı��ϣ�ֱ��д��HD��GC��EB�Ľ��������д������̣���
��2����ͼ��1���е�������AEGH�Ƶ�A��תһ���Ƕȣ���ͼ��2������HD��GC��EB��
��3����ͼ��2���е������ζ����ɾ��Σ���ͼ��3��������֪DA��AB=HA��AE=m��n����ʱHD��GC��EB��ֵ�루2��С��Ľ������б仯������б仯��ֱ��д���仯��Ľ��������д������̣���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ������ֵ����ʽ|x|��3��|x|��3�Ľ⼯�Ĺ��̣�
��Ϊ|x|��3������ͼ1��ʾ�������Ͽ�������-3��С��3�����ľ���ֵ��С��3�ģ�����|x|��3�Ľ⼯��-3��x��3��
��Ϊ|x|��3������ͼ2��ʾ�������Ͽ���С����-3�����ʹ���3�����ľ���ֵ�Ǵ���3�ģ�����|x|��3�Ľ⼯��x��-3��x��3��

�����������⣺
��1������ʽ|x|��a��a��0���Ľ⼯Ϊ______������ʽ|x|��a��a��0���Ľ⼯Ϊ______��
��2���ⲻ��ʽ|x-5|��3��
��3���ⲻ��ʽ|x-3|��5��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com