
【题目】如图,AD∥BC,∠A=90°,E是![]() 上的一点,且
上的一点,且![]() ,
,![]() .
.

(1)判断![]() 的形状,并说明理由.
的形状,并说明理由.
(2)若![]() ,
,![]() ,请求出
,请求出![]() 的长.
的长.
【答案】(1)等腰直角三角形;(2)![]() .
.
【解析】
(1)求出∠A=∠B,证出△DAE≌△EBC,推出DE=EC,再证明∠DEC=90°即可;
(2)根据全等三角形性质得出AD=BE=3,AE=BC=9﹣3=6.在Rt△AED中,由勾股定理求出DE,由∠DEC=90°,根据勾股定理求出即可.
(1)△DEC是等腰直角三角形.理由如下:
∵AD∥BC,∴∠A+∠B=180°.
∵∠A=90°,∴∠B=90°=∠A,
在△ADE和△BEC中,∵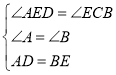 ,∴△DAE≌△EBC,∴DE=EC.
,∴△DAE≌△EBC,∴DE=EC.
∵∠B=90°,∴∠BEC+∠BCE=90°.
∵∠AED=∠BCE,∴∠BEC+∠AED=90°,∴∠DEC=90°,
∴△DEC是等腰直角三角形.
(2)∵AD=3,AB=9,△DAE≌△EBC,∴AD=BE=3,AE=BC=9﹣3=6.
在Rt△AED中,由勾股定理得:![]() .
.
在Rt△DEC中,由勾股定理得:DC![]()
![]() .
.


 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:
【题目】如图,在7×7网格中,每个小正方形的边长都为1.

(1)若点A(1,3),C(2,1), ①建立适当的平面直角坐标系;②点B的坐标为( , );
(2)判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校决定在学生中开设:A、实心球;B、立定跳远;C、跳绳;D、跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图,请结合图中的信息解答下列问题:

(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整.
(3)若调查到喜欢“跳绳”的5名学生中有2名男生,3名女生,现从这5名学生中任意抽取2名学生,请用画树状图或列表法求出刚好抽到不同性别学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
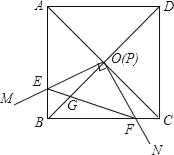
【题目】如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G.
(1)求四边形OEBF的面积;
(2)求证:OGBD=EF2;
(3)在旋转过程中,当△BEF与△COF的面积之和最大时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲打字员计划用若干小时完成文稿的电脑输入工作,两小时后,乙打字员协助此项工作,且乙打字员文稿电脑输入的速度是甲的1.5倍,结果提前6小时完成任务,则甲打字员原计划完成此项工作的时间是( )
A.17小时B.14小时C.12小时D.10小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,点D是弧BC的中点,PD切⊙O于点D.
(1)求证:DP⊥AP;
(2)若PD=![]() ,PC=1,求图中阴影部分的面积.(结果保留π)
,PC=1,求图中阴影部分的面积.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D,E,F分别在边BC,AC,AB上,且BD=CE,DC=BF,连结DE,EF,DF,∠1=60°

(1)求证:△BDF≌△CED.
(2)判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为开拓学生视野,开展“课外读书周”活动,活动后期随机调查了九年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题:

(1)本次调查的学生总数为_____人,被调查学生的课外阅读时间的中位数是_____小时,众数是_____小时;并补全条形统计图;
(2)在扇形统计图中,课外阅读时间为5小时的扇形的圆心角度数是_____;
(3)若全校九年级共有学生800人,估计九年级一周课外阅读时间为6小时的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com