
分析 (1)设租用甲种汽车x辆,则租用乙种汽车(10-x)辆,根据题意列出不等式组,求得答案即可.
(2)分别计算甲、乙所需要的费用,然后比较,花费较少的即为最省钱的租车方案.
解答 解:(1)设租用甲种汽车x辆,则租用乙种汽车(10-x)辆,
由题意得:$\left\{\begin{array}{l}{40x+30(10-x)≥350}\\{16x+20(10-x)≥165}\end{array}\right.$,
解得:5≤x≤8$\frac{3}{4}$,
x是整数,x可取5、6、7、8,
即共有,4种租车方案:
方案一:租用甲种汽车5辆,乙种汽车5辆;
方案二:租用甲种汽车6辆,乙种汽车4辆;
方案三:租用甲种汽车7辆,乙种汽车3辆;
方案四:租用甲种汽车8辆,乙种汽车2辆.
(2)解法一:
第一种租车方案的费用为5×2000+5×1800=19000(元);
第二种租车方案的费用为6×2000+4×1800=19200(元);
第三种租车方案的费用为7×2000+3×1800=19400(元);
第四种租车方案的费用为8×2000+2×1800=19600(元).
因此租用甲种汽车5辆,乙种汽车5辆的方案更省费用.
解法二:设总的租车费用为y元,
y=2000x+1800(10-x)=18000+200x,5≤x≤6.
∵200>0,
∴y随x增大而增大,
∴当x=5时,取得最小值,y=5×2000+5×1800=19000(元);
∴租用甲种汽车5辆,乙种汽车5辆的方案更省费用.
点评 本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.准确的找到不等关系列不等式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
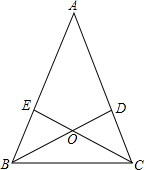 如图,在△ABC中,AB=AC,分别根据以下条件,说明△OBC是等腰三角形.
如图,在△ABC中,AB=AC,分别根据以下条件,说明△OBC是等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
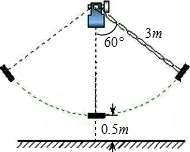 如图所示,秋千链子的长度为3m,静止时秋千踏板(大小忽略不计)距地面0.5m,秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°,则秋千踏板与地面的最大距离约为多少?
如图所示,秋千链子的长度为3m,静止时秋千踏板(大小忽略不计)距地面0.5m,秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°,则秋千踏板与地面的最大距离约为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示为在场地上画平行线的简单方法,将皮带尺从P拉到A,取AP的中点M,并且在点M上竖一木桩,再将皮带从n上的另一点B拉向M,使它过M,取MC=BM,那么过P、C两点的直线m就是平行于n的一条直线,为什么?
如图所示为在场地上画平行线的简单方法,将皮带尺从P拉到A,取AP的中点M,并且在点M上竖一木桩,再将皮带从n上的另一点B拉向M,使它过M,取MC=BM,那么过P、C两点的直线m就是平行于n的一条直线,为什么?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
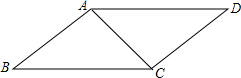 如图,已知平行四边形ABCD中,AB=40cm,AC=30cm,BC=50cm,有一动点P从点B出发,以1cm/秒的速度沿B→C→D运动至D点停止,当运动时间为20或25或14或80秒时,以P,A,C为顶点的三角形是等腰三角形.
如图,已知平行四边形ABCD中,AB=40cm,AC=30cm,BC=50cm,有一动点P从点B出发,以1cm/秒的速度沿B→C→D运动至D点停止,当运动时间为20或25或14或80秒时,以P,A,C为顶点的三角形是等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com