
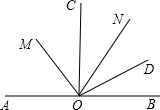
 如图,∠AOC=90°,ON是锐角∠COD的平分线,OM是∠AOD的平分线,求∠MON的度数.
如图,∠AOC=90°,ON是锐角∠COD的平分线,OM是∠AOD的平分线,求∠MON的度数.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
| A、47.5 kg<x<48.5 kg |
| B、47 kg<x<49 kg |
| C、47.5 kg≤x<48.5 kg |
| D、47.5 kg<x≤48.5 kg |
查看答案和解析>>
科目:初中数学 来源: 题型:
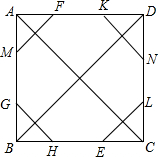 如图,木工要用一个正方形木板制成一个正八边形采取了如下方式作图:先确定正方形ABCD的中心O,再分别以A、B、C、D为圆心,AO为半径作弧和各边相交于F、M、E、H、G、L、N、K,你认为木工的作图可得到一个八边形吗?若能,试证明;若不能,说明理由.
如图,木工要用一个正方形木板制成一个正八边形采取了如下方式作图:先确定正方形ABCD的中心O,再分别以A、B、C、D为圆心,AO为半径作弧和各边相交于F、M、E、H、G、L、N、K,你认为木工的作图可得到一个八边形吗?若能,试证明;若不能,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、四边形的外角和大于内角和 |
| B、一个多边形的内角和为1880° |
| C、一个多边形的内角中,锐角的个数可以任意多 |
| D、若多边形边数从3增加到n(n为大于3的自然数),它们的外角和度数不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB1路线爬行,则下列结论正确的是( )
图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB1路线爬行,则下列结论正确的是( )| A、甲先到B点 |
| B、乙先到B点 |
| C、甲、乙同时到B |
| D、无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
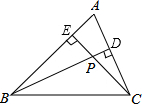 如图,在△ABC中,高BD和CE相交于点P.
如图,在△ABC中,高BD和CE相交于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com