
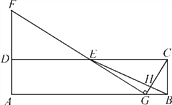
【题目】如图,在矩形ABCD中,E为CD的中点,H为BE上的一点, ![]() =3,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
=3,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
(1)求证: ![]() ;
;
(2)若∠CGF=90°,求![]() 的值.
的值.
【答案】(1)证明见解析;(2) ![]() =3
=3![]() .
.
【解析】试题分析:(1)根据相似三角形判定的方法,判断出△CEH∽△GBH,即可推得结论;
(2)作EM⊥AB于M,则EM=BC=AD,AM=DE,设DE=CE=3a,则AB=CD=6a,由(1)得: ![]() =3,得出BG=
=3,得出BG=![]() CE=a,AG=5a,证明△DEF∽△GEC,由相似三角形的性质得出EGEF=DEEC,由平行线证出
CE=a,AG=5a,证明△DEF∽△GEC,由相似三角形的性质得出EGEF=DEEC,由平行线证出![]() =
=![]() ,得出EF=
,得出EF=![]() EG,求出EG=
EG,求出EG=![]() a,在Rt△EMG中,GM=2a,由勾股定理求出BC=EM=
a,在Rt△EMG中,GM=2a,由勾股定理求出BC=EM=![]() a,即可得出结果.
a,即可得出结果.
试题解析:解:(1)∵四边形ABCD是矩形,∴CD∥AB,AD=BC,AB=CD,AD∥BC,∴△CEH∽△GBH,∴ ![]() .
.
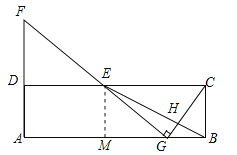
(2)作EM⊥AB于M,如图所示:
则EM=BC=AD,AM=DE,∵E为CD的中点,∴DE=CE,设DE=CE=3a,则AB=CD=6a,由(1)得: ![]() =3,∴BG=
=3,∴BG=![]() CE=a,∴AG=5a,∵∠EDF=90°=∠CGF,∠DEF=∠GEC,∴△DEF∽△GEC,∴
CE=a,∴AG=5a,∵∠EDF=90°=∠CGF,∠DEF=∠GEC,∴△DEF∽△GEC,∴![]() ,∴EGEF=DEEC,∵CD∥AB,∴
,∴EGEF=DEEC,∵CD∥AB,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴EF=
,∴EF=![]() EG,∴EG
EG,∴EG![]() EG=3a3a,解得:EG=
EG=3a3a,解得:EG=![]() a,在Rt△EMG中,GM=2a,∴EM=
a,在Rt△EMG中,GM=2a,∴EM=![]() =
=![]() a,∴BC=
a,∴BC=![]() a,∴
a,∴![]() =
=![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
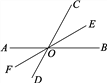
【题目】如图,直线AB、CD相交于点O,OE平分∠BOC,∠BOC=70°,OF是OE的反向延长线.
(1)求∠DOF与∠BOF的度数;
(2)OF平分∠AOD吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b与坐标轴交于C,D两点,直线AB与坐标轴交于A,B两点,线段OA,OC的长是方程x2﹣3x+2=0的两个根(OA>OC).
(1)求点A,C的坐标;
(2)直线AB与直线CD交于点E,若点E是线段AB的中点,反比例函数y=![]() (k≠0)的图象的一个分支经过点E,求k的值;
(k≠0)的图象的一个分支经过点E,求k的值;
(3)在(2)的条件下,点M在直线CD上,坐标平面内是否存在点N,使以点B,E,M,N为顶点的四边形是菱形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】巴黎与北京的时差为﹣7小时(正数表示同一时刻比北京时间早的时数),如果北京时间11月11日14:00,那么巴黎时间是( )
A.11月11日21时
B.11月11日7时
C.11月10日7时
D.11月11日5时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,O是矩形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE、CE相交于点E.求证: 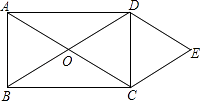
(1)四边形OCED是菱形.
(2)连接OE,若AD=4,CD=3,求菱形OCED的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
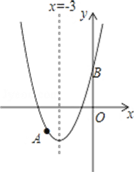
【题目】如图,抛物线y=x2+bx+c过点A(﹣4,﹣3),与y轴交于点B,对称轴是x=﹣3,请解答下列问题:
(1)求抛物线的解析式.
(2)若和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,求△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的边BC与x轴重合,连接对角线BD交y轴于点E,过点A作AG⊥BD于点G,直线GF交AD于点F,AB、OC的长分别是一元二次方程x-5x+6=0的两根(AB>OC),且tan∠ADB=![]() .
.
(1)求点E、点G的坐标;
(2)直线GF分△AGD为△AGF与△DGF两个三角形,且S△AGF:S△DGF =3:1,求直线GF的解析式;
(3)点P在y轴上,在坐标平面内是否存在一点Q,使以点B、D、P、Q为顶点的四边形是矩形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
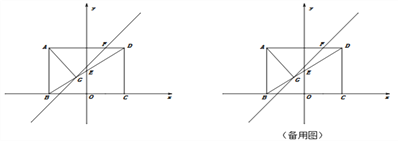
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料360kg,乙种原料290kg,计划用这两种原料生产A、B两种产品共50件,已知生产一件A种产品,需用甲种原料9kg,乙种原料3kg,可获利润700元;生产一件B种产品,需用甲种原料4kg,乙种原料10kg,可获利润1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润是W(元),采用哪种生产方案获总利润最大?最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com