
【题目】如图,在平面直角坐标系中,△ABC的顶点A在x轴负半轴上,顶点C在x轴正半轴上,顶点B在第一象限,线段OA,OC的长是一元二次方程x2-12x+36=0的两根,BC=4![]() ,∠BAC=45°.
,∠BAC=45°.
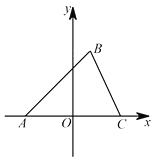
(1)直接写出点A的坐标________点 C的坐标________;
(2)若反比例函数y=![]() 的图象经过点B,求k的值;
的图象经过点B,求k的值;
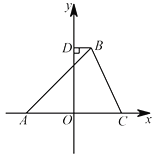
(3)如图过点B作BD⊥y轴于点D;在y轴上是否存在点P,使以P,B,D为顶点的三角形与以P, O,A为顶点的三角形相似?若存在,直接写出满足条件的点P的坐标;若不存在,请说明理由.
【答案】(1)(-6,0),(6,0);(2)k=16;(3)点P的坐标为:(0,2)或(0,6)或(0,12)或(0,4+2![]() )或(0,4-2
)或(0,4-2![]() ).
).
【解析】
(1)首先利用直接开平方法求出方程 x2-12x+36=0的两根,从而得出OA=OC=6,进而得出A、C两点的坐标;
(2)如图,过点B作BE⊥AC,垂足为E, 根据等腰直角三角形的性质得出AE=BE, 设BE=x,EC=12-x, 在RtΔBEC中利用勾股定理建立方程,求解并检验即可得出BE、OE的长从而得出B点的坐标,然后利用待定系数法即可求出反比例函数的解析式;
(3)存在.如图2,若点P在OD上,若△PDB∽△AOP,根据相似三角形对应边成比例得出![]() ,根据比例式列出方程,求解即可得出P点的坐标;如图3,若点P在OD上方,△PDB∽△AOP, 根据相似三角形对应边成比例得出
,根据比例式列出方程,求解即可得出P点的坐标;如图3,若点P在OD上方,△PDB∽△AOP, 根据相似三角形对应边成比例得出![]() ,则根据比例式列出方程,求解并检验即可得出P点的坐标;如图4,若点P在OD上方,△PDB∽△AOP,根据相似三角形对应边成比例得出
,则根据比例式列出方程,求解并检验即可得出P点的坐标;如图4,若点P在OD上方,△PDB∽△AOP,根据相似三角形对应边成比例得出![]() ,根据比例式列出方程,求解并检验即可得出P点的坐标;如图5,若点P在y轴负半轴,△PDB∽△AOP,根据相似三角形对应边成比例得出
,根据比例式列出方程,求解并检验即可得出P点的坐标;如图5,若点P在y轴负半轴,△PDB∽△AOP,根据相似三角形对应边成比例得出![]() ,根据比例式列出方程,求解并检验即可得出P点的坐标,综上所述即可得出答案.
,根据比例式列出方程,求解并检验即可得出P点的坐标,综上所述即可得出答案.
(1)解一元二次方程 x2-12x+36=0,
解得:x1=x2=6 ,
所以OA=OC=6 ,
故答案为:A(-6,0),C(6,0);
(2)如图,过点B作BE⊥AC,垂足为E,
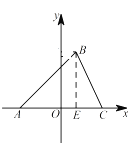
∵∠BAC=45°,
∴AE=BE,
设BE=x,
∵AE+CE=OA+OC=12,
∴EC=12-x,
在RtΔBEC中,BC=![]() ,
,
∴![]() ,
,
整理得:x2-12x+32=0,
解得:x1=4 (不合题意舍去),x2=8,
∴ BE=8,OE=8-6=2,
∴B(2,8),
把B(2,8)代入![]() ,得k=16,
,得k=16,
(3)存在,
如图2,
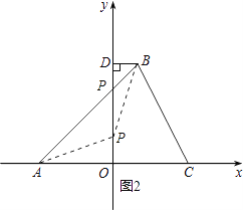
若点P在OD上,若△PDB∽△AOP,
则 ![]() ,即
,即![]() ,
,
解得:OP=2或OP=6,
∴P(0,2)或P(0,6);
如图3,
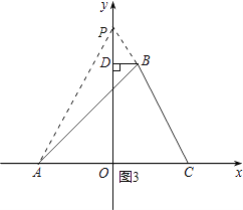
若点P在OD上方,△PDB∽△AOP,
则 ![]() ,即
,即 ![]() ,
,
解得:OP=12,
∴P(0,12);
如图4,
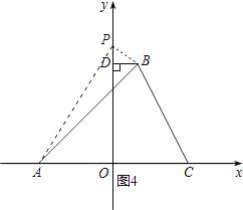
若点P在OD上方,△BDP∽△AOP,
则 ![]() ,即
,即 ![]() ,
,
解得:OP=4+2![]() 或OP=4-2
或OP=4-2![]() (不合题意舍去),
(不合题意舍去),
∴P(0,4+2![]() );
);
如图5,
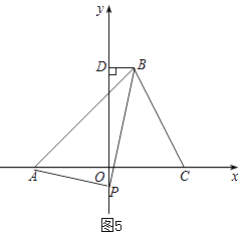
若点P在y轴负半轴,△PDB∽△AOP,
则![]() ,即
,即 ![]() ,
,
解得:OP=-4+2![]() 或-4-2
或-4-2![]() (不合题意舍去),
(不合题意舍去),
则P点坐标为(0,4-2![]() )
)
故点P的坐标为:(0,2)或(0,6)或(0,12)或(0,4+2![]() )或(0,4-2
)或(0,4-2![]() ).
).


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
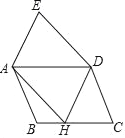
【题目】如图,将平行四边形ABCD绕点D旋转,点C落在BC上的点H处,点B恰好落在点A处,得平行四边形DHAE,若BH=2,CH=3,则DC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,∠BAD是△ABC的一个外角,∠BAC、∠BAD的平分线分别交⊙O于点E、F.请你在图上连接EF.(1)证明:EF是⊙O的直径;(2)请你判断EF与BC有怎样的位置关系?并请证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
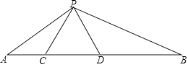
【题目】如图,在![]() 中,点
中,点![]() 、
、![]() 在边
在边![]() 上,
上,![]() ,
,![]() .
.
![]() 试说明
试说明![]() 与
与![]() 相似.
相似.
![]() 若
若![]() ,
,![]() ,
,![]() ,请你求出
,请你求出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
![]() 小明猜想:若
小明猜想:若![]() ,
,![]() ,
,![]() ,只要
,只要![]() 与
与![]() 之间满足某种关系式,问题
之间满足某种关系式,问题![]() 中的函数关系式仍然成立.你同意小明的观点吗?如果你同意,请求出
中的函数关系式仍然成立.你同意小明的观点吗?如果你同意,请求出![]() 与
与![]() 所满足的关系式;若不同意,请说明理由.
所满足的关系式;若不同意,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
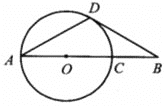
【题目】如图,线段AB经过圆心O,交⊙O于点A、C,点D在⊙O上,连接AD,BD,∠A=∠B=30°.
证明:(1)BD是⊙O的切线
(2)如果BD=2求OC的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系(如图1所示).

(1)求出这条抛物线的函数解析式,并写出自变量x的取值范围;
(2)隧道下的公路是双向行车道(正中间是一条宽1米的隔离带),其中的一条行车道能否行驶宽2.5米、高5米的特种车辆?请通过计算说明;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”CDAB,使A、D点在抛物线上。B、C点在地面OM线上(如图2所示).为了筹备材料,需测算“脚手架”三根钢杆AB、AD、DC的长度之和的最大值是多少,请你帮施工队计算一下.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )

A. (11﹣2![]() )米 B. (11
)米 B. (11![]() ﹣2
﹣2![]() )米 C. (11﹣2
)米 C. (11﹣2![]() )米 D. (11
)米 D. (11![]() ﹣4)米
﹣4)米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com