练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，四边形ABCD是平行四边形，P是CD上一点，且AP和BP分别平分∠DAB和∠CBA.

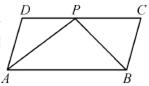
    (1)求∠APB的度数；

    (2)如果AD=5 cm，AP=8 cm，求△APB的周长.


    (1)∵ABCD是平行四边形，

    ∴AD∥CB，AB∥CD，

    ∴∠DAB+∠CBA=180°.

    又∵AP和BP分别平分∠DAB和∠CBA，

    ∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°，

    ∴∠APB=180°-(∠PAB+∠PBA)=90°.

    (2)∵AP平分∠DAB且AB∥CD，

    ∴∠DAP=∠PAB=∠DPA.

    ∴△ADP是等腰三角形.

    ∴AD=DP=5 cm.

    同理PC=CB=5 cm，∴AB=DP+PC=10 cm.

    在Rt△APB中，AB=10 cm，AP=8 cm，

    ∴BP==6(cm).

    ∴△APB的周长是6+8+10=24(cm).


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2014-2015学年江苏省江阴市八年级上学期期末调研考试数学试卷（解析版） 题型：填空题

    如图，在△ABC中，AB＝AC＝5，BC＝6，点E、F是中线AD上的两点，则图中阴影部分的面积是

    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，一只猫头鹰蹲在一棵树AC的点B（点B在AC上）处，发现一只老鼠躲进短墙DF的另一侧，猫头鹰的视线被短墙遮住.为了寻找这只老鼠，它又飞至树顶C处.已知短墙高DF=4米，短墙底部D与树的底部A的距离AD=2.7米，猫头鹰从C点观测F点的俯角为53°，老鼠躲藏处M距D点3米，且点M在DE上.

    (参考数据：sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)

    (1)猫头鹰飞至C处后，能否看到这只老鼠？为什么？

    (2)要捕捉到这只老鼠，猫头鹰至少要飞多少米(精确到0.1米)？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，□ABCD中，下列说法一定正确的是(     )

    A.AC=BD      B.AC⊥BD      C.AB=CD       D.AB=BC

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，以△ABC的顶点A为圆心，以BC长为半径作弧，再以顶点C为圆心，以AB长为半径作弧，两弧交于点D，连接AD，CD.若∠B=65°，则∠ADC的大小为          度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


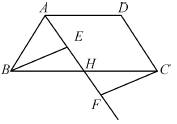
    如图，在四边形ABCD中，点H是边BC的中点，作射线AH，在线段AH及其延长线上分别取点E,F，连接BE,CF.

    (1)请你添加一个条件，使得△BEH≌△CFH，你添加的条件是       ，并证明；

    (2)在问题(1)中，当BH与EH满足什么关系时，四边形BFCE是矩形，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，菱形ABCD中，∠A=60°，BD=7，则菱形ABCD的周长为          .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，菱形ABCD中，AB=4，∠B=60°，AE⊥BC,AF⊥CD，垂足分别为E,F，连接EF，则△AEF的面积是          .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC的顶点A、B、C均在⊙O上，若∠ABC+∠AOC=90°，则∠AOC的大小是(     )

    A.30°               B.45°              C.60°                  D.70°

    查看答案和解析>>

    同步练习册答案