
分析 (1)把对应的特殊角的三角函数值代入化简计算.
(2)根据已知和特殊角的三角函数值求得a+b=$\frac{\sqrt{2}+\sqrt{3}}{2}$,a-b=$\frac{\sqrt{2}-\sqrt{3}}{2}$,代入化简后的分式计算.
解答 解:(1)原式=6×($\frac{1}{2}$)2-$\sqrt{3}$×$\frac{\sqrt{3}}{2}$-2×$\frac{\sqrt{2}}{2}$
=-$\sqrt{2}$.
(2)$\frac{{a}^{2}+ab}{{a}^{2}+2ab+{b}^{2}}$-(a-b)÷$\frac{({a}^{2}-{b}^{2})}{b}$
=$\frac{a(a+b)}{(a+b)^{2}}$-(a-b)×$\frac{b}{(a+b)(a-b)}$
=$\frac{a}{a+b}$-$\frac{b}{a+b}$=$\frac{a-b}{a+b}$.
∵a=sin45°=$\frac{\sqrt{2}}{2}$,b=sin60°=$\frac{\sqrt{3}}{2}$,
∴a+b=$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{2}+\sqrt{3}}{2}$,a-b=$\frac{\sqrt{2}-\sqrt{3}}{2}$
∴原式=$\frac{\frac{\sqrt{2}-\sqrt{3}}{2}}{\frac{\sqrt{2}+\sqrt{3}}{2}}$=2$\sqrt{6}$-5.
点评 考查特殊角三角函数值的计算,特殊角三角函数值计算在中考中经常出现.解题关键是熟记特殊角的三角函数值.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
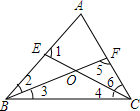 如图所示,在△ABC中,E、F分别在AB、AC上,则下列各式不能成立的是( )
如图所示,在△ABC中,E、F分别在AB、AC上,则下列各式不能成立的是( )| A. | ∠BOC=∠2+∠6+∠A | B. | ∠2=∠5-∠A | C. | ∠5=∠1+∠A | D. | ∠1=∠ABC+∠4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com